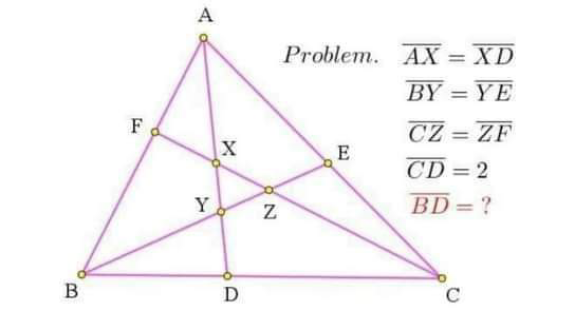
Question Number 206640 by cortano21 last updated on 21/Apr/24
Answered by mr W last updated on 21/Apr/24

Commented by mr W last updated on 21/Apr/24

$$\frac{{EY}}{{YB}}×\frac{{x}}{\mathrm{2}}×\frac{{y}+{z}}{{z}}=\mathrm{1} \\ $$$$\Rightarrow\frac{{y}}{{z}}=\frac{\mathrm{2}}{{x}}−\mathrm{1}=\frac{\mathrm{2}−{x}}{{x}} \\ $$$$\frac{{FZ}}{{ZC}}×\frac{{y}}{{z}}×\frac{{p}+{q}}{{q}}=\mathrm{1} \\ $$$$\frac{\mathrm{2}−{x}}{{x}}×\left(\mathrm{1}+\frac{{p}}{{q}}\right)=\mathrm{1} \\ $$$$\Rightarrow\frac{{p}}{{q}}=\frac{{x}}{\mathrm{2}−{x}}−\mathrm{1}=\frac{\mathrm{2}\left({x}−\mathrm{1}\right)}{\mathrm{2}−{x}} \\ $$$$\frac{{DX}}{{XA}}×\frac{{p}}{{q}}×\frac{{x}+\mathrm{2}}{\mathrm{2}}=\mathrm{1} \\ $$$$\frac{\mathrm{2}\left({x}−\mathrm{1}\right)}{\mathrm{2}−{x}}×\frac{{x}+\mathrm{2}}{\mathrm{2}}=\mathrm{1} \\ $$$${x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{4}=\mathrm{0} \\ $$$$\Rightarrow{x}=\sqrt{\mathrm{5}}−\mathrm{1}\:\checkmark \\ $$
Answered by A5T last updated on 21/Apr/24

$$\frac{{BD}}{{DC}}=\frac{{k}}{\mathrm{2}};\frac{{BC}}{{DC}}=\frac{{k}+\mathrm{2}}{\mathrm{2}} \\ $$$$\frac{{AF}}{{FB}}×\frac{{BC}}{{CD}}×\frac{{DX}}{{AX}}=\mathrm{1}\Rightarrow\frac{{AF}}{{FB}}=\frac{\mathrm{2}}{{k}+\mathrm{2}}\Rightarrow\frac{{FB}}{{BA}}=\frac{{k}+\mathrm{2}}{\mathrm{4}+{k}} \\ $$$$\frac{{AE}}{{EC}}×\frac{{CZ}}{{ZF}}×\frac{{FB}}{{BA}}=\mathrm{1}\Rightarrow\frac{{AE}}{{EC}}=\frac{\mathrm{4}+{k}}{{k}+\mathrm{2}} \\ $$$$\frac{{BD}}{{DC}}×\frac{{CA}}{{AE}}×\frac{{EY}}{{EB}}=\mathrm{1}\Rightarrow\frac{\left({k}\right)\left(\mathrm{6}+\mathrm{2}{k}\right)}{\mathrm{2}\left(\mathrm{4}+{k}\right)}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{6}{k}+\mathrm{2}{k}^{\mathrm{2}} =\mathrm{8}+\mathrm{2}{k}\Rightarrow{k}^{\mathrm{2}} −\mathrm{2}{k}−\mathrm{4}=\mathrm{0}\Rightarrow{k}=\sqrt{\mathrm{5}}−\mathrm{1} \\ $$
