Question Number 206677 by mr W last updated on 22/Apr/24
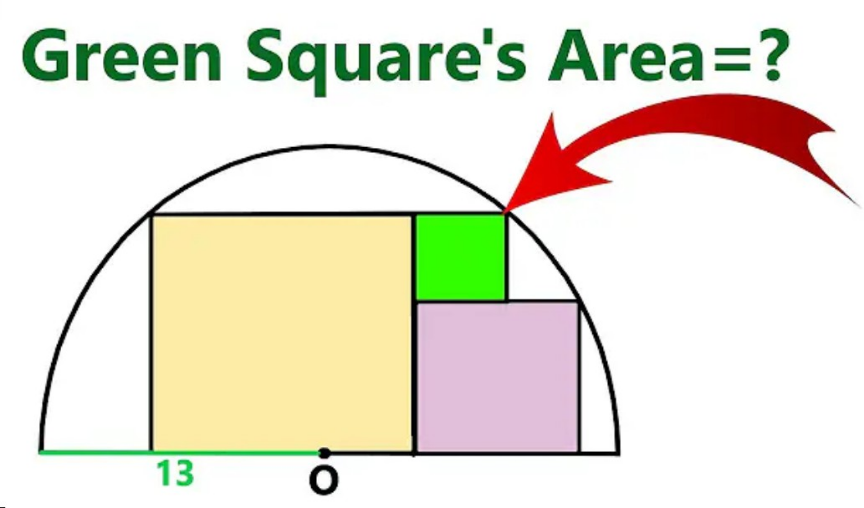
Answered by mr W last updated on 22/Apr/24

Commented by mr W last updated on 23/Apr/24

$${b}={a}−{c} \\ $$$$\sqrt{{R}^{\mathrm{2}} −{b}^{\mathrm{2}} }={a}+{b}−\sqrt{{R}^{\mathrm{2}} −{a}^{\mathrm{2}} } \\ $$$$\Rightarrow{b}=\sqrt{{R}^{\mathrm{2}} −{a}^{\mathrm{2}} } \\ $$$$\frac{{a}+{c}}{\mathrm{2}}=\sqrt{{R}^{\mathrm{2}} −{a}^{\mathrm{2}} } \\ $$$$\frac{{a}+{c}}{\mathrm{2}}={b}={a}−{c} \\ $$$$\Rightarrow{a}=\mathrm{3}{c} \\ $$$$\frac{\mathrm{3}{c}+{c}}{\mathrm{2}}=\sqrt{{R}^{\mathrm{2}} −\left(\mathrm{3}{c}\right)^{\mathrm{2}} } \\ $$$$\mathrm{4}{c}^{\mathrm{2}} ={R}^{\mathrm{2}} −\mathrm{9}{c}^{\mathrm{2}} \\ $$$$\Rightarrow{c}^{\mathrm{2}} =\frac{{R}^{\mathrm{2}} }{\mathrm{13}}=\mathrm{13}\:={area}\:{of}\:{green}\:{square} \\ $$
Answered by A5T last updated on 23/Apr/24

Commented by A5T last updated on 23/Apr/24

$$\left({a}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} +\left({b}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} +{R}^{\mathrm{2}} \Rightarrow{a}^{\mathrm{2}} +{b}^{\mathrm{2}} ={R}^{\mathrm{2}} =\mathrm{169} \\ $$$${c}={a}−{b}\:\wedge\:\frac{{a}+{c}}{\mathrm{2}}=\sqrt{{R}^{\mathrm{2}} −{a}^{\mathrm{2}} }\Rightarrow\frac{\mathrm{2}{a}−{b}}{\mathrm{2}}={b}\Rightarrow\mathrm{3}{b}=\mathrm{2}{a} \\ $$$$\Rightarrow\left(\mathrm{2}{a}\right)^{\mathrm{2}} +\mathrm{4}{b}^{\mathrm{2}} =\mathrm{169}×\mathrm{4}\Rightarrow{b}^{\mathrm{2}} =\mathrm{13}×\mathrm{4}\Rightarrow{a}^{\mathrm{2}} =\mathrm{13}×\mathrm{9} \\ $$$$\Rightarrow{c}=\mathrm{3}\sqrt{\mathrm{13}}−\mathrm{2}\sqrt{\mathrm{13}}=\sqrt{\mathrm{13}}\Rightarrow{c}^{\mathrm{2}} =\mathrm{13} \\ $$
