Question Number 206704 by mr W last updated on 22/Apr/24
Commented by mr W last updated on 22/Apr/24

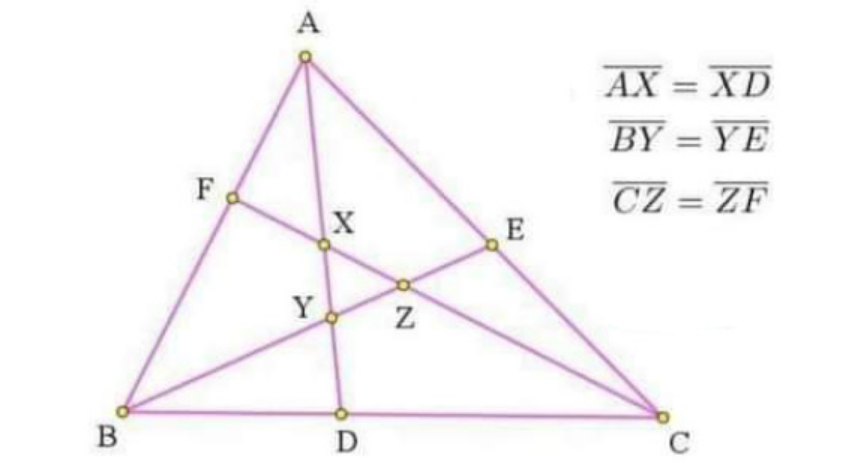
$${find}\:\frac{\Delta_{{XYZ}} }{\Delta_{{ABC}} }=? \\ $$
Answered by A5T last updated on 22/Apr/24
![BD=x;DC=y ((AE)/(EC))×((CZ)/(ZF))×((FB)/(BA))=1⇒((AE)/(EC))=((BA)/(FB))=((x+2y)/(x+y)) ((CD)/(DB))×((BY)/(YE))×((EA)/(AC))=1⇒(y/x)=((CD)/(DB))=((AC)/(EA)) ((BF)/(FA))×((AX)/(XD))×((DC)/(CB))=1⇒((BF)/(FA))=((BC)/(DC))=((x+y)/y) ⇒((AE)/(EC))×((CD)/(DB))×((BF)/(FA))=((x+2y)/x) ⇒(([XYZ])/([ABC]))=(((1−((x+2y)/x))^2 )/((1+((x+2y)/(x+y))+((y(x+2y))/(x(x+y))))(1+(y/x)+((x+y)/x))(1+((x+y)/y)+((x+2y)/y)))) =(y^3 /(2(x+2y)(x+y)^2 ))](https://www.tinkutara.com/question/Q206708.png)
$${BD}={x};{DC}={y} \\ $$$$\frac{{AE}}{{EC}}×\frac{{CZ}}{{ZF}}×\frac{{FB}}{{BA}}=\mathrm{1}\Rightarrow\frac{{AE}}{{EC}}=\frac{{BA}}{{FB}}=\frac{{x}+\mathrm{2}{y}}{{x}+{y}} \\ $$$$\frac{{CD}}{{DB}}×\frac{{BY}}{{YE}}×\frac{{EA}}{{AC}}=\mathrm{1}\Rightarrow\frac{{y}}{{x}}=\frac{{CD}}{{DB}}=\frac{{AC}}{{EA}} \\ $$$$\frac{{BF}}{{FA}}×\frac{{AX}}{{XD}}×\frac{{DC}}{{CB}}=\mathrm{1}\Rightarrow\frac{{BF}}{{FA}}=\frac{{BC}}{{DC}}=\frac{{x}+{y}}{{y}} \\ $$$$\Rightarrow\frac{{AE}}{{EC}}×\frac{{CD}}{{DB}}×\frac{{BF}}{{FA}}=\frac{{x}+\mathrm{2}{y}}{{x}} \\ $$$$\Rightarrow\frac{\left[{XYZ}\right]}{\left[{ABC}\right]}=\frac{\left(\mathrm{1}−\frac{{x}+\mathrm{2}{y}}{{x}}\right)^{\mathrm{2}} }{\left(\mathrm{1}+\frac{{x}+\mathrm{2}{y}}{{x}+{y}}+\frac{{y}\left({x}+\mathrm{2}{y}\right)}{{x}\left({x}+{y}\right)}\right)\left(\mathrm{1}+\frac{{y}}{{x}}+\frac{{x}+{y}}{{x}}\right)\left(\mathrm{1}+\frac{{x}+{y}}{{y}}+\frac{{x}+\mathrm{2}{y}}{{y}}\right)} \\ $$$$=\frac{{y}^{\mathrm{3}} }{\mathrm{2}\left({x}+\mathrm{2}{y}\right)\left({x}+{y}\right)^{\mathrm{2}} } \\ $$
Commented by A5T last updated on 23/Apr/24
![((AC)/(EA))=(y/x) ∧ ((AC)/(EA))=((2x+3y)/(x+2y)) ⇒(y/x)=((2x+3y)/(x+2y))⇒y=((x((√5)+1))/2) ⇒(([XYZ])/([ABC]))=((7−3(√5))/4)≈0.07295](https://www.tinkutara.com/question/Q206714.png)
$$\frac{{AC}}{{EA}}=\frac{{y}}{{x}}\:\wedge\:\frac{{AC}}{{EA}}=\frac{\mathrm{2}{x}+\mathrm{3}{y}}{{x}+\mathrm{2}{y}} \\ $$$$\Rightarrow\frac{{y}}{{x}}=\frac{\mathrm{2}{x}+\mathrm{3}{y}}{{x}+\mathrm{2}{y}}\Rightarrow{y}=\frac{{x}\left(\sqrt{\mathrm{5}}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$$\Rightarrow\frac{\left[{XYZ}\right]}{\left[{ABC}\right]}=\frac{\mathrm{7}−\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{4}}\approx\mathrm{0}.\mathrm{07295} \\ $$
Commented by mr W last updated on 23/Apr/24
��
Answered by mr W last updated on 23/Apr/24

Commented by mr W last updated on 23/Apr/24
![((EY)/(YB))×(a/b)×((c+d)/d)=1 ⇒(c/d)=(b/a)−1=λ−1 with λ=(b/a) ((FZ)/(ZC))×(c/d)×((p+q)/q)=1 ⇒(λ−1)(1+(p/q))=1 ⇒(p/q)=(1/(λ−1))−1 ((DX)/(XA))×(p/q)×((a+b)/b)=1 ⇒((1/(λ−1))−1)(1+(1/λ))=1 ⇒λ^2 −λ−1=0 ⇒λ=((1+(√5))/2)=ϕ (golden ratio) (similarly (d/c)=(q/p)=λ) let μ=((ZY)/(YB))=((XZ)/(ZC))=((YX)/(XA)) ((ZY)/(YB))×(a/b)×((CX)/(XZ))=1 ⇒μ×(1/λ)×((1/μ)+1)=1 ⇒μ=λ−1=(((√5)−1)/2)=(1/λ) [ΔADC]=(b/(a+b))[ΔABC]=(λ/(1+λ))[ΔABC] [ΔCXD]=(([ΔADC])/2)=(λ/(2(1+λ)))[ΔABC] [ΔCYX]=((XY)/(YD))[ΔCDX]=μ[ΔCDX]=((μλ)/(2(1+λ)))[ΔABC] [ΔXYZ]=((XZ)/(XC))[ΔCYX]=(μ/(1+μ))[ΔCYX]=((μ^2 λ)/(2(1+μ)(1+λ)))[ΔABC] ⇒(([ΔXYZ])/([ΔABC]))=((μ^2 λ)/(2(1+μ)(1+λ)))=(1/(2λ^4 )) =((7−3(√5))/4)≈0.07295](https://www.tinkutara.com/question/Q206713.png)
$$\frac{{EY}}{{YB}}×\frac{{a}}{{b}}×\frac{{c}+{d}}{{d}}=\mathrm{1} \\ $$$$\Rightarrow\frac{{c}}{{d}}=\frac{{b}}{{a}}−\mathrm{1}=\lambda−\mathrm{1}\:{with}\:\lambda=\frac{{b}}{{a}} \\ $$$$\frac{{FZ}}{{ZC}}×\frac{{c}}{{d}}×\frac{{p}+{q}}{{q}}=\mathrm{1} \\ $$$$\Rightarrow\left(\lambda−\mathrm{1}\right)\left(\mathrm{1}+\frac{{p}}{{q}}\right)=\mathrm{1}\:\Rightarrow\frac{{p}}{{q}}=\frac{\mathrm{1}}{\lambda−\mathrm{1}}−\mathrm{1} \\ $$$$\frac{{DX}}{{XA}}×\frac{{p}}{{q}}×\frac{{a}+{b}}{{b}}=\mathrm{1} \\ $$$$\Rightarrow\left(\frac{\mathrm{1}}{\lambda−\mathrm{1}}−\mathrm{1}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\lambda}\right)=\mathrm{1} \\ $$$$\Rightarrow\lambda^{\mathrm{2}} −\lambda−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\lambda=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}=\varphi\:\left({golden}\:{ratio}\right) \\ $$$$\left({similarly}\:\frac{{d}}{{c}}=\frac{{q}}{{p}}=\lambda\right) \\ $$$${let}\:\mu=\frac{{ZY}}{{YB}}=\frac{{XZ}}{{ZC}}=\frac{{YX}}{{XA}} \\ $$$$\frac{{ZY}}{{YB}}×\frac{{a}}{{b}}×\frac{{CX}}{{XZ}}=\mathrm{1} \\ $$$$\Rightarrow\mu×\frac{\mathrm{1}}{\lambda}×\left(\frac{\mathrm{1}}{\mu}+\mathrm{1}\right)=\mathrm{1} \\ $$$$\Rightarrow\mu=\lambda−\mathrm{1}=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\lambda} \\ $$$$\left[\Delta{ADC}\right]=\frac{{b}}{{a}+{b}}\left[\Delta{ABC}\right]=\frac{\lambda}{\mathrm{1}+\lambda}\left[\Delta{ABC}\right] \\ $$$$\left[\Delta{CXD}\right]=\frac{\left[\Delta{ADC}\right]}{\mathrm{2}}=\frac{\lambda}{\mathrm{2}\left(\mathrm{1}+\lambda\right)}\left[\Delta{ABC}\right] \\ $$$$\left[\Delta{CYX}\right]=\frac{{XY}}{{YD}}\left[\Delta{CDX}\right]=\mu\left[\Delta{CDX}\right]=\frac{\mu\lambda}{\mathrm{2}\left(\mathrm{1}+\lambda\right)}\left[\Delta{ABC}\right] \\ $$$$\left[\Delta{XYZ}\right]=\frac{{XZ}}{{XC}}\left[\Delta{CYX}\right]=\frac{\mu}{\mathrm{1}+\mu}\left[\Delta{CYX}\right]=\frac{\mu^{\mathrm{2}} \lambda}{\mathrm{2}\left(\mathrm{1}+\mu\right)\left(\mathrm{1}+\lambda\right)}\left[\Delta{ABC}\right] \\ $$$$\Rightarrow\frac{\left[\Delta{XYZ}\right]}{\left[\Delta{ABC}\right]}=\frac{\mu^{\mathrm{2}} \lambda}{\mathrm{2}\left(\mathrm{1}+\mu\right)\left(\mathrm{1}+\lambda\right)}=\frac{\mathrm{1}}{\mathrm{2}\lambda^{\mathrm{4}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{7}−\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{4}}\approx\mathrm{0}.\mathrm{07295} \\ $$
