Question Number 206794 by MaruMaru last updated on 25/Apr/24
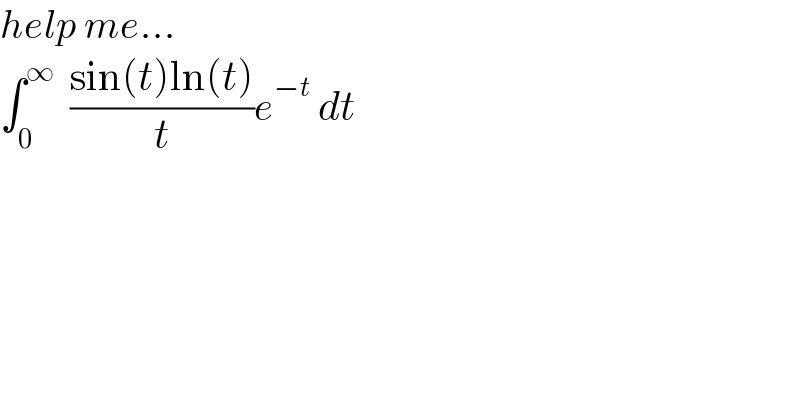
$${help}\:{me}… \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{sin}\left({t}\right)\mathrm{ln}\left({t}\right)}{{t}}{e}^{−{t}} \:{dt} \\ $$
Answered by Berbere last updated on 25/Apr/24
![let f(a)=∫_0 ^∞ (1/t)sin(at)ln(t)e^(−t) dt a∈R f is defined f(0)=0 We want f(1) we can verifie That f is C_1 ∀t∈]0,∞[ a→^g ((sin(at))/t)ln(t)e^(−t) is deivable ∀a∈R t→((sin(at))/t)ln(t)e^(−t) is integrabe g′(a)=cos(at)ln(t)e^(−t) ∣g′(a)∣≤∣ln(t)∣e^(−t) ;∀a∈R ∫_0 ^∞ ∣ln(t)∣e^(−t) dt<∞⇒we can switch ∂ and ∫ f′(a)=∫_0 ^∞ cos(at)ln(t)e^(−t) =Re∫_0 ^∞ ln(t)e^(t(−1+ia)) dt introduce h(z)=∫_0 ^∞ t^z e^(t(−1+ia)) ;z≥0 f′(a)=h′(z)∣_(z=0) h(z)=^((−1+ia)t→t) −∫_0 ^∞ ((t^z e^(−t) )/((−1+ia)^(z+1) ))dt=((Γ(1+z))/((−1+ia)^(z+1) )) f′(a)=h′(a)=−((Γ′(1)(−1+ia)−ln(−1+ia)(−1+ia))/((−1+ia)^2 )) =−(((Γ′(1))/(−1+ia))−((ln(−1+ia))/(−1+ia)));Γ′(1)=−γ∴Γ′(1)=Γ(1)Ψ(1)=1.−γ f′(a)=−Re((γ/(1−ia))+((ln(−1+ia))/(1−ia))) Re is lineair f(1)=∫_0 ^1 f′(a)da;=−Re∫_0 ^1 ((γ/(1−ia))+((ln(−1+ia))/(1−ia)))da =−Re[(γ/(−i))ln(1−ia)+(1/(−2i))ln^2 (−1+ia)]_0 ^1 =−Re[γiln(1−i)+(i/2)ln^2 (1−i)−(i/2)ln^2 (−1)] log(z)=ln∣z∣ +i arg(z);z∈]−π,π] =−Re(γi(ln((√2))−((iπ)/4)+(i/2)(ln(√2)−((iπ)/4))^2 −(i/2)(iπ)^2 ) =−(((γπ)/4)+(π/4)ln((√2)))=−(π/4)γ−((πln(2))/8) ∫_0 ^∞ ((sin(t)ln(t)e^(−t) )/t)dt=−(π/4)(γ+((ln(2))/2))](https://www.tinkutara.com/question/Q206803.png)
$${let}\:{f}\left({a}\right)=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{{t}}{sin}\left({at}\right){ln}\left({t}\right){e}^{−{t}} {dt}\:\:{a}\in\mathbb{R}\:{f}\:{is}\:{defined} \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{0}\:{We}\:{want}\:{f}\left(\mathrm{1}\right) \\ $$$${we}\:{can}\:{verifie}\:{That}\:{f}\:{is}\:{C}_{\mathrm{1}} \\ $$$$\left.\forall{t}\in\right]\mathrm{0},\infty\left[\:{a}\overset{{g}} {\rightarrow}\frac{{sin}\left({at}\right)}{{t}}{ln}\left({t}\right){e}^{−{t}} \:{is}\:{deivable}\right. \\ $$$$\forall{a}\in\mathbb{R}\:{t}\rightarrow\frac{{sin}\left({at}\right)}{{t}}{ln}\left({t}\right){e}^{−{t}} \:{is}\:{integrabe} \\ $$$${g}'\left({a}\right)={cos}\left({at}\right){ln}\left({t}\right){e}^{−{t}} \\ $$$$\mid{g}'\left({a}\right)\mid\leqslant\mid{ln}\left({t}\right)\mid{e}^{−{t}} ;\forall{a}\in\mathbb{R} \\ $$$$\int_{\mathrm{0}} ^{\infty} \mid{ln}\left({t}\right)\mid{e}^{−{t}} {dt}<\infty\Rightarrow{we}\:{can}\:{switch}\:\partial\:{and}\:\int \\ $$$${f}'\left({a}\right)=\int_{\mathrm{0}} ^{\infty} {cos}\left({at}\right){ln}\left({t}\right){e}^{−{t}} ={Re}\int_{\mathrm{0}} ^{\infty} {ln}\left({t}\right){e}^{{t}\left(−\mathrm{1}+{ia}\right)} {dt} \\ $$$${introduce}\:{h}\left({z}\right)=\int_{\mathrm{0}} ^{\infty} {t}^{{z}} {e}^{{t}\left(−\mathrm{1}+{ia}\right)} ;{z}\geqslant\mathrm{0} \\ $$$${f}'\left({a}\right)={h}'\left({z}\right)\mid_{{z}=\mathrm{0}} \\ $$$${h}\left({z}\right)\overset{\left(−\mathrm{1}+{ia}\right){t}\rightarrow{t}} {=}−\int_{\mathrm{0}} ^{\infty} \frac{{t}^{{z}} {e}^{−{t}} }{\left(−\mathrm{1}+{ia}\right)^{{z}+\mathrm{1}} }{dt}=\frac{\Gamma\left(\mathrm{1}+{z}\right)}{\left(−\mathrm{1}+{ia}\right)^{{z}+\mathrm{1}} } \\ $$$${f}'\left({a}\right)={h}'\left({a}\right)=−\frac{\Gamma'\left(\mathrm{1}\right)\left(−\mathrm{1}+{ia}\right)−{ln}\left(−\mathrm{1}+{ia}\right)\left(−\mathrm{1}+{ia}\right)}{\left(−\mathrm{1}+{ia}\right)^{\mathrm{2}} } \\ $$$$=−\left(\frac{\Gamma'\left(\mathrm{1}\right)}{−\mathrm{1}+{ia}}−\frac{{ln}\left(−\mathrm{1}+{ia}\right)}{−\mathrm{1}+{ia}}\right);\Gamma'\left(\mathrm{1}\right)=−\gamma\therefore\Gamma'\left(\mathrm{1}\right)=\Gamma\left(\mathrm{1}\right)\Psi\left(\mathrm{1}\right)=\mathrm{1}.−\gamma \\ $$$${f}'\left({a}\right)=−{Re}\left(\frac{\gamma}{\mathrm{1}−{ia}}+\frac{{ln}\left(−\mathrm{1}+{ia}\right)}{\mathrm{1}−{ia}}\right) \\ $$$${Re}\:{is}\:{lineair}\: \\ $$$${f}\left(\mathrm{1}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {f}'\left({a}\right){da};=−{Re}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\gamma}{\mathrm{1}−{ia}}+\frac{{ln}\left(−\mathrm{1}+{ia}\right)}{\mathrm{1}−{ia}}\right){da} \\ $$$$=−{Re}\left[\frac{\gamma}{−{i}}{ln}\left(\mathrm{1}−{ia}\right)+\frac{\mathrm{1}}{−\mathrm{2}{i}}{ln}^{\mathrm{2}} \left(−\mathrm{1}+{ia}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=−{Re}\left[\gamma{iln}\left(\mathrm{1}−{i}\right)+\frac{{i}}{\mathrm{2}}{ln}^{\mathrm{2}} \left(\mathrm{1}−{i}\right)−\frac{{i}}{\mathrm{2}}{ln}^{\mathrm{2}} \left(−\mathrm{1}\right)\right] \\ $$$$\left.{l}\left.{og}\left({z}\right)={ln}\mid{z}\mid\:+{i}\:{arg}\left({z}\right);{z}\in\right]−\pi,\pi\right]\: \\ $$$$=−{Re}\left(\gamma{i}\left({ln}\left(\sqrt{\mathrm{2}}\right)−\frac{{i}\pi}{\mathrm{4}}+\frac{{i}}{\mathrm{2}}\left({ln}\sqrt{\mathrm{2}}−\frac{{i}\pi}{\mathrm{4}}\right)^{\mathrm{2}} −\frac{{i}}{\mathrm{2}}\left({i}\pi\right)^{\mathrm{2}} \right)\right. \\ $$$$=−\left(\frac{\gamma\pi}{\mathrm{4}}+\frac{\pi}{\mathrm{4}}{ln}\left(\sqrt{\mathrm{2}}\right)\right)=−\frac{\pi}{\mathrm{4}}\gamma−\frac{\pi{ln}\left(\mathrm{2}\right)}{\mathrm{8}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left({t}\right){ln}\left({t}\right){e}^{−{t}} }{{t}}{dt}=−\frac{\pi}{\mathrm{4}}\left(\gamma+\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}}\right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by MaruMaru last updated on 26/Apr/24

$$°\smile°\:\:{good}\:{thx}! \\ $$
