Question Number 206788 by SANOGO last updated on 25/Apr/24

Answered by A5T last updated on 25/Apr/24
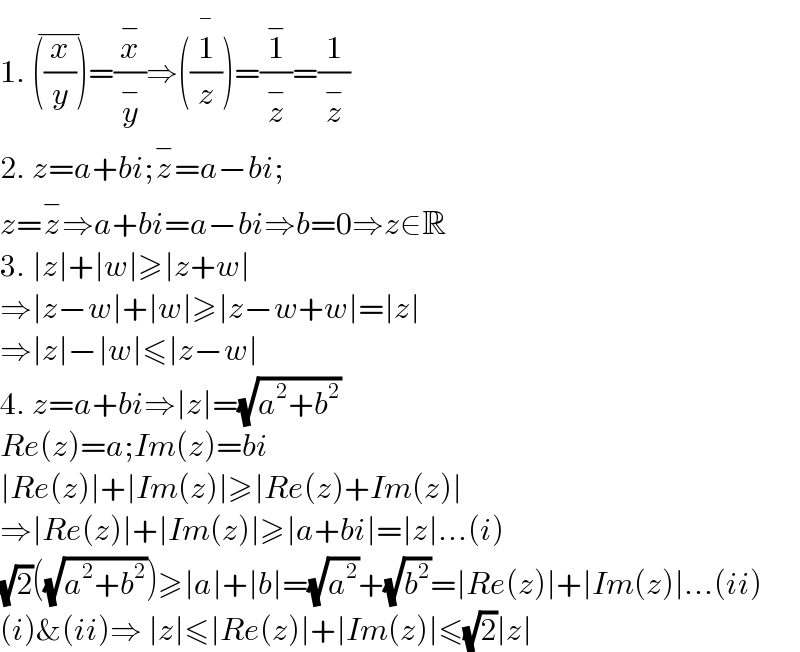
$$\mathrm{1}.\:\overline {\left(\frac{{x}}{{y}}\right)}=\frac{\overset{−} {{x}}}{\overset{−} {{y}}}\Rightarrow\overset{�} {\left(\frac{\mathrm{1}}{{z}}\right)}=\frac{\overset{−} {\mathrm{1}}}{\overset{−} {{z}}}=\frac{\mathrm{1}}{\overset{−} {{z}}} \\ $$$$\mathrm{2}.\:{z}={a}+{bi};\overset{−} {{z}}={a}−{bi};\: \\ $$$${z}=\overset{−} {{z}}\Rightarrow{a}+{bi}={a}−{bi}\Rightarrow{b}=\mathrm{0}\Rightarrow{z}\in\mathbb{R} \\ $$$$\mathrm{3}.\:\mid{z}\mid+\mid{w}\mid\geqslant\mid{z}+{w}\mid \\ $$$$\Rightarrow\mid{z}−{w}\mid+\mid{w}\mid\geqslant\mid{z}−{w}+{w}\mid=\mid{z}\mid \\ $$$$\Rightarrow\mid{z}\mid−\mid{w}\mid\leqslant\mid{z}−{w}\mid \\ $$$$\mathrm{4}.\:{z}={a}+{bi}\Rightarrow\mid{z}\mid=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$${Re}\left({z}\right)={a};{Im}\left({z}\right)={bi} \\ $$$$\mid{Re}\left({z}\right)\mid+\mid{Im}\left({z}\right)\mid\geqslant\mid{Re}\left({z}\right)+{Im}\left({z}\right)\mid \\ $$$$\Rightarrow\mid{Re}\left({z}\right)\mid+\mid{Im}\left({z}\right)\mid\geqslant\mid{a}+{bi}\mid=\mid{z}\mid…\left({i}\right) \\ $$$$\sqrt{\mathrm{2}}\left(\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\right)\geqslant\mid{a}\mid+\mid{b}\mid=\sqrt{{a}^{\mathrm{2}} }+\sqrt{{b}^{\mathrm{2}} }=\mid{Re}\left({z}\right)\mid+\mid{Im}\left({z}\right)\mid…\left({ii}\right) \\ $$$$\left({i}\right)\&\left({ii}\right)\Rightarrow\:\mid{z}\mid\leqslant\mid{Re}\left({z}\right)\mid+\mid{Im}\left({z}\right)\mid\leqslant\sqrt{\mathrm{2}}\mid{z}\mid \\ $$
