Question-206795

Question Number 206795 by BaliramKumar last updated on 25/Apr/24

Commented by BaliramKumar last updated on 25/Apr/24

$$\mathrm{can}\:\mathrm{be}\:\:\left(\mathrm{a}\right)\:\mathrm{right}??? \\ $$

Commented by A5T last updated on 25/Apr/24

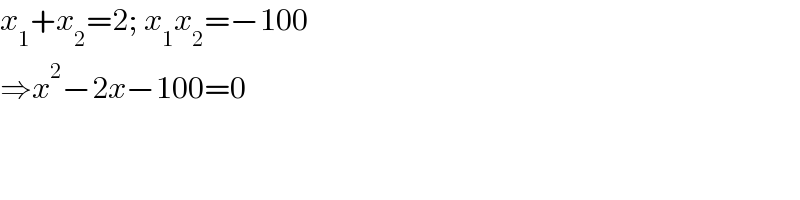
x_1 +x_2 =2; x_1 x_2 =−100 ⇒x^2 −2x−100=0

$${x}_{\mathrm{1}} +{x}_{\mathrm{2}} =\mathrm{2};\:{x}_{\mathrm{1}} {x}_{\mathrm{2}} =−\mathrm{100} \\ $$$$\Rightarrow{x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{100}=\mathrm{0} \\ $$

Commented by A5T last updated on 25/Apr/24

Let the quadratic equation be f(x)=ax^2 +bx+c Then ((−b)/a)=2; (c/a)=−100 ⇒f(x)=a(x^2 −2x−100) x_1 +x_2 =2⇒x_1 =2−x_2 x_1 x_2 =−100⇒(2−x_2 )x_2 =100⇒x_2 ^2 −2x_2 −100=0 ⇒x_2 =1+_− (√(101)) ⇒(x_1 ,x_2 )=(1+(√(101)),1−(√(101))) upto symmetry. The roots will always be the same for all polynomials, so it may contradict (a) which wants it to have different roots.

$${Let}\:{the}\:{quadratic}\:{equation}\:{be}\:{f}\left({x}\right)={ax}^{\mathrm{2}} +{bx}+{c} \\ $$$${Then}\:\frac{−{b}}{{a}}=\mathrm{2};\:\:\frac{{c}}{{a}}=−\mathrm{100} \\ $$$$\Rightarrow{f}\left({x}\right)={a}\left({x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{100}\right) \\ $$$${x}_{\mathrm{1}} +{x}_{\mathrm{2}} =\mathrm{2}\Rightarrow{x}_{\mathrm{1}} =\mathrm{2}−{x}_{\mathrm{2}} \\ $$$${x}_{\mathrm{1}} {x}_{\mathrm{2}} =−\mathrm{100}\Rightarrow\left(\mathrm{2}−{x}_{\mathrm{2}} \right){x}_{\mathrm{2}} =\mathrm{100}\Rightarrow{x}_{\mathrm{2}} ^{\mathrm{2}} −\mathrm{2}{x}_{\mathrm{2}} −\mathrm{100}=\mathrm{0} \\ $$$$\Rightarrow{x}_{\mathrm{2}} =\mathrm{1}\underset{−} {+}\sqrt{\mathrm{101}} \\ $$$$\Rightarrow\left({x}_{\mathrm{1}} ,{x}_{\mathrm{2}} \right)=\left(\mathrm{1}+\sqrt{\mathrm{101}},\mathrm{1}−\sqrt{\mathrm{101}}\right)\:{upto}\:{symmetry}. \\ $$$$ \\ $$$${The}\:{roots}\:{will}\:{always}\:{be}\:{the}\:{same}\:{for}\:{all}\: \\ $$$${polynomials},\:{so}\:{it}\:{may}\:{contradict}\:\left({a}\right)\:{which} \\ $$$${wants}\:{it}\:{to}\:{have}\:{different}\:{roots}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply