Question-206924

Question Number 206924 by mr W last updated on 01/May/24

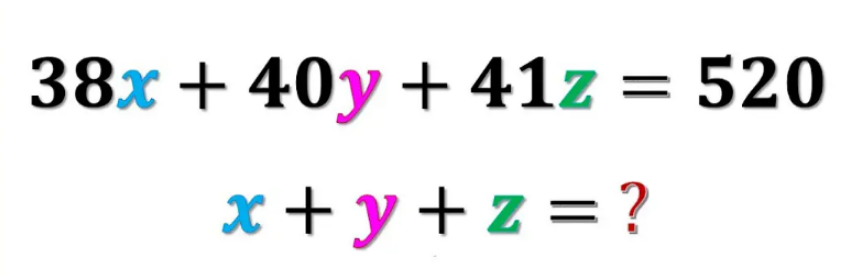
Commented by mr W last updated on 01/May/24

x, y, z \in N

Answered by MATHEMATICSAM last updated on 01/May/24

38 (x + y + z) ⩽ 38 x + 40 y + 41 z

or, 38 (x + y + z) ⩽ 520

or, x + y + z ⩽ \frac{520}{38} = 13.68 \dots (i)

41 (x + y + z) ⩾ 38 x + 40 y + 41 z

or, 41 (x + y + z) ⩾ 520

or, x + y + z ⩾ \frac{520}{41} = 12.68 \dots (ii)

From (i) and (ii)

12.68 ⩽ x + y + z ⩽ 13.68

x, y, z \in N

∴ x + y + z = 13 (Ans)

Commented by mr W last updated on 01/May/24

t h a n k s!

Answered by A5T last updated on 01/May/24

z = 2 k \Rightarrow 38 x + 40 y + 82 k = 520

\Rightarrow 19 x + 20 y + 41 k = 260 \Rightarrow k ⩽ 6

19 x + 41 k \equiv 0 (m o d 10) \Rightarrow k \equiv x (m o d 10)

- x + k \equiv 0 (m o d 20) \Rightarrow x = k

\Rightarrow 19 k + 20 y + 41 k = 20 y + 60 k = 260

\Rightarrow y + 3 k = 13 \Rightarrow y = 13 - 3 k

19 k + 20 (13 - 3 k) + 41 k = 260 \Rightarrow x = k = 0 \Rightarrow y = 13

\Rightarrow x + y + z = 13

Facebook Tweet Pin