Question Number 207292 by mr W last updated on 10/May/24
Commented by mr W last updated on 10/May/24

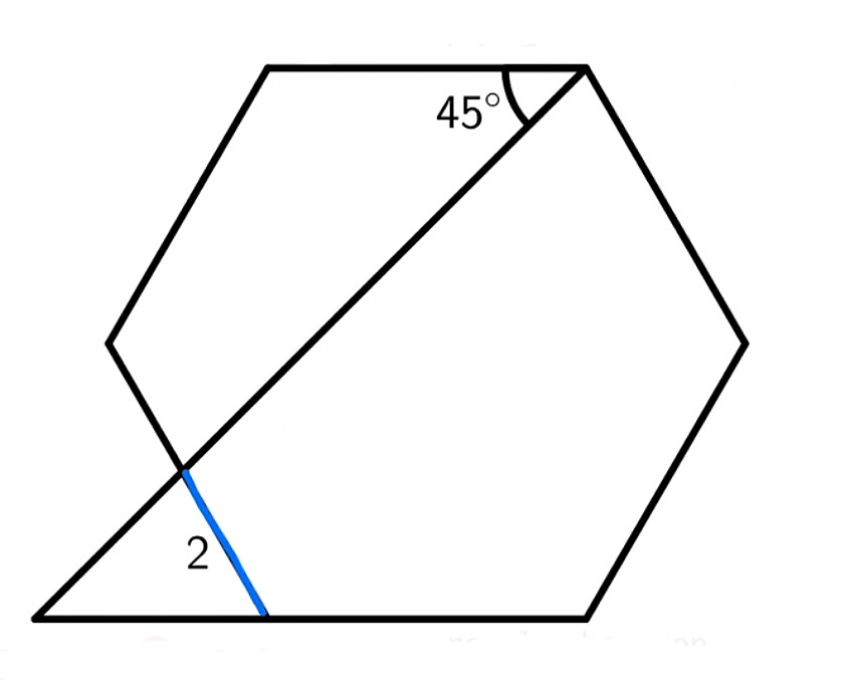
$${find}\:{the}\:{side}\:{length}\:{of}\:{the}\:{regular} \\ $$$${hexagon}. \\ $$
Answered by A5T last updated on 10/May/24

Commented by A5T last updated on 10/May/24

$${DC}={AC}={s}\sqrt{\mathrm{3}}\Rightarrow{AB}={s}\sqrt{\mathrm{3}}−{s}={s}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right) \\ $$$$\frac{{sin}\mathrm{45}°}{\mathrm{2}}=\frac{{sin}\mathrm{75}°}{{s}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)}\Rightarrow{s}=\mathrm{2}+\sqrt{\mathrm{3}} \\ $$
Commented by mr W last updated on 11/May/24
��
Answered by mr W last updated on 11/May/24

Commented by mr W last updated on 11/May/24

$${x}=\sqrt{\mathrm{3}}{a}−{a} \\ $$$$\frac{\mathrm{2}{a}−\mathrm{2}}{\mathrm{2}}=\frac{\mathrm{2}{a}}{\:\sqrt{\mathrm{3}}{a}−{a}} \\ $$$$\Rightarrow{a}=\mathrm{2}+\sqrt{\mathrm{3}} \\ $$
Answered by mr W last updated on 11/May/24

Commented by mr W last updated on 11/May/24

$$\frac{{y}}{\mathrm{2}}=\frac{{AB}}{{AC}}=\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{2}{a}}\:\Rightarrow{y}=\sqrt{\mathrm{3}} \\ $$$${a}=\mathrm{2}+\sqrt{\mathrm{3}} \\ $$
