Question Number 144791 by imjagoll last updated on 29/Jun/21

$$\:\mathrm{Express}\:\mathrm{sin}\:\mathrm{5x}\:\mathrm{as}\:\mathrm{polynomial} \\ $$$$\:\mathrm{in}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{sin}\:\mathrm{x}.\: \\ $$
Answered by liberty last updated on 29/Jun/21
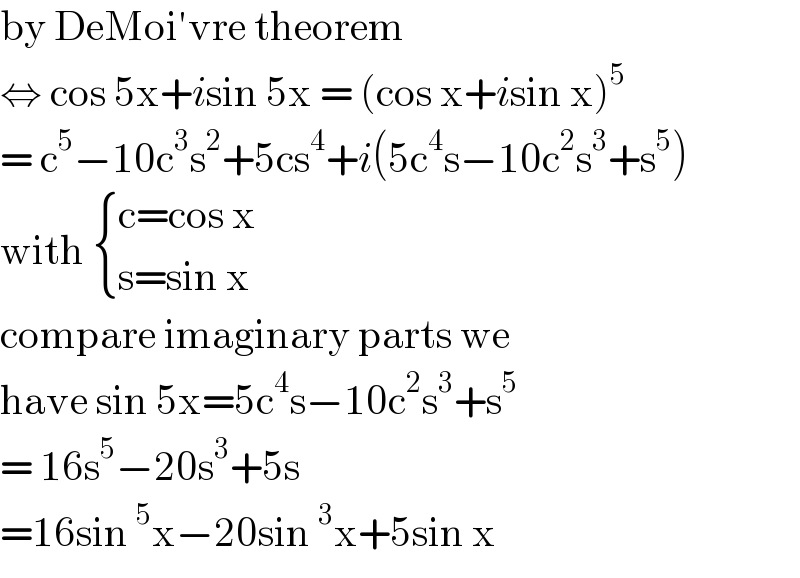
$$\mathrm{by}\:\mathrm{DeMoi}'\mathrm{vre}\:\mathrm{theorem} \\ $$$$\Leftrightarrow\:\mathrm{cos}\:\mathrm{5x}+{i}\mathrm{sin}\:\mathrm{5x}\:=\:\left(\mathrm{cos}\:\mathrm{x}+{i}\mathrm{sin}\:\mathrm{x}\right)^{\mathrm{5}} \\ $$$$=\:\mathrm{c}^{\mathrm{5}} −\mathrm{10c}^{\mathrm{3}} \mathrm{s}^{\mathrm{2}} +\mathrm{5cs}^{\mathrm{4}} +{i}\left(\mathrm{5c}^{\mathrm{4}} \mathrm{s}−\mathrm{10c}^{\mathrm{2}} \mathrm{s}^{\mathrm{3}} +\mathrm{s}^{\mathrm{5}} \right) \\ $$$$\mathrm{with}\:\begin{cases}{\mathrm{c}=\mathrm{cos}\:\mathrm{x}}\\{\mathrm{s}=\mathrm{sin}\:\mathrm{x}}\end{cases} \\ $$$$\mathrm{compare}\:\mathrm{imaginary}\:\mathrm{parts}\:\mathrm{we} \\ $$$$\mathrm{have}\:\mathrm{sin}\:\mathrm{5x}=\mathrm{5c}^{\mathrm{4}} \mathrm{s}−\mathrm{10c}^{\mathrm{2}} \mathrm{s}^{\mathrm{3}} +\mathrm{s}^{\mathrm{5}} \\ $$$$=\:\mathrm{16s}^{\mathrm{5}} −\mathrm{20s}^{\mathrm{3}} +\mathrm{5s}\: \\ $$$$=\mathrm{16sin}\:^{\mathrm{5}} \mathrm{x}−\mathrm{20sin}\:^{\mathrm{3}} \mathrm{x}+\mathrm{5sin}\:\mathrm{x}\: \\ $$
