Question Number 144985 by imjagoll last updated on 01/Jul/21
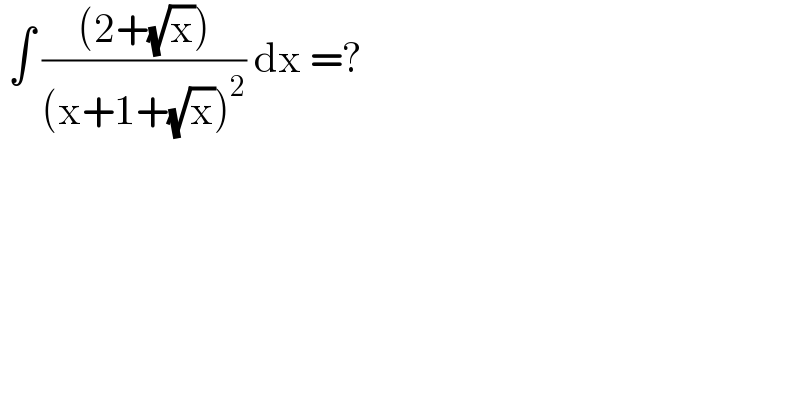
$$\:\int\:\frac{\left(\mathrm{2}+\sqrt{\mathrm{x}}\right)}{\left(\mathrm{x}+\mathrm{1}+\sqrt{\mathrm{x}}\right)^{\mathrm{2}} }\:\mathrm{dx}\:=? \\ $$
Answered by mathmax by abdo last updated on 01/Jul/21

$$\mathrm{f}\left(\mathrm{a}\right)=\int\:\:\:\frac{\mathrm{2}+\sqrt{\mathrm{x}}}{\mathrm{x}+\mathrm{a}+\sqrt{\mathrm{x}}}\:\:\:\mathrm{with}\:\mathrm{a}>\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{a}\right)=−\int\:\:\frac{\mathrm{2}+\sqrt{\mathrm{x}}}{\left(\mathrm{x}+\mathrm{a}+\sqrt{\mathrm{x}}\right)^{\mathrm{2}} }\mathrm{dx}\:\Rightarrow \\ $$$$−\mathrm{f}^{'} \left(\mathrm{1}\right)=\int\:\:\frac{\mathrm{2}+\sqrt{\mathrm{x}}}{\left(\mathrm{x}+\mathrm{1}+\sqrt{\mathrm{x}}\right)^{\mathrm{2}} }\mathrm{dx}\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=_{\sqrt{\mathrm{x}}=\mathrm{t}} \:\:\:\int\:\:\:\frac{\mathrm{2}+\mathrm{t}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{a}+\mathrm{t}}\left(\mathrm{2t}\right)\mathrm{dt}\:=\int\:\:\frac{\mathrm{2t}+\mathrm{t}^{\mathrm{2}} }{\mathrm{t}^{\mathrm{2}} \:+\mathrm{t}+\mathrm{a}}\mathrm{dt} \\ $$$$=\int\:\frac{\mathrm{t}^{\mathrm{2}} +\mathrm{t}+\mathrm{a}\:+\mathrm{t}−\mathrm{a}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{t}+\mathrm{a}}\mathrm{dt}\:=\mathrm{t}\:+\int\:\:\frac{\mathrm{t}−\mathrm{a}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{t}+\mathrm{a}}\mathrm{dt} \\ $$$$\mathrm{t}^{\mathrm{2}} +\mathrm{t}+\mathrm{a}=\mathrm{0}\:\Rightarrow\Delta=\mathrm{1}−\mathrm{4a}\:<\mathrm{0}\:\mathrm{because}\:\mathrm{a}>\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow \\ $$$$\int\:\:\frac{\mathrm{t}−\mathrm{a}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{t}+\mathrm{a}}\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\frac{\mathrm{2t}+\mathrm{1}−\mathrm{2a}−\mathrm{1}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{t}+\mathrm{a}}\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{2t}+\mathrm{1}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{t}+\mathrm{a}}\mathrm{dt}−\frac{\mathrm{2a}+\mathrm{1}}{\mathrm{2}}\int\:\:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{t}+\mathrm{a}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{t}+\mathrm{a}\right)−\frac{\mathrm{2a}+\mathrm{1}}{\mathrm{2}}\mathrm{I} \\ $$$$\mathrm{I}=\int\:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{2}\frac{\mathrm{t}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{a}−\frac{\mathrm{1}}{\mathrm{4}}}=\int\:\frac{\mathrm{dt}}{\left(\mathrm{t}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{4a}−\mathrm{1}}{\mathrm{4}}} \\ $$$$=_{\mathrm{t}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{4a}−\mathrm{1}}}{\mathrm{2}}\mathrm{y}} \:\:\:\:\int\:\:\frac{\mathrm{1}}{\left(\frac{\mathrm{4a}−\mathrm{1}}{\mathrm{4}}\right)\left(\mathrm{1}+\mathrm{y}^{\mathrm{2}} \right)}\frac{\sqrt{\mathrm{4a}−\mathrm{1}}}{\mathrm{2}}\mathrm{dy} \\ $$$$=\frac{\mathrm{2}\sqrt{\mathrm{4a}−\mathrm{1}}}{\mathrm{4a}−\mathrm{1}}\:\mathrm{arctany}\:+\mathrm{c}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}\mathrm{arctan}\left(\frac{\mathrm{2t}+\mathrm{1}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}\right)+\mathrm{c}\Rightarrow \\ $$$$\int\:\frac{\mathrm{t}−\mathrm{a}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{t}+\mathrm{a}}\mathrm{dt}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{t}+\mathrm{a}\right)−\frac{\mathrm{2a}+\mathrm{1}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}\mathrm{arctan}\left(\frac{\mathrm{2t}+\mathrm{1}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}\right)\:+\mathrm{c}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\sqrt{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\left(\mathrm{x}+\sqrt{\mathrm{x}}+\mathrm{a}\right)−\frac{\mathrm{2a}+\mathrm{1}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}\mathrm{arctan}\left(\frac{\mathrm{2}\sqrt{\mathrm{x}}+\mathrm{1}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}\right)\:+\mathrm{c}\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{x}+\sqrt{\mathrm{x}}+\mathrm{a}\right)}−\left(\frac{\mathrm{2}\sqrt{\mathrm{4a}−\mathrm{1}}−\left(\mathrm{2a}+\mathrm{1}\right)\frac{\mathrm{2}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}}{\mathrm{4a}−\mathrm{1}}\right)\mathrm{arctan}\left(\frac{\mathrm{2}\sqrt{\mathrm{x}}+\mathrm{1}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}\right) \\ $$$$−\left(\frac{\mathrm{2a}+\mathrm{1}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}\right)×\frac{\left(\mathrm{2}\sqrt{\mathrm{x}}+\mathrm{1}\right)\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}\right)^{'} }{\mathrm{1}+\left(\frac{\mathrm{2}\sqrt{\mathrm{x}}+\mathrm{1}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{x}+\sqrt{\mathrm{x}}+\mathrm{a}\right)}−\frac{\mathrm{2}\left(\mathrm{4a}−\mathrm{1}\right)−\mathrm{2}\left(\mathrm{2a}+\mathrm{1}\right)}{\left(\mathrm{4a}−\mathrm{1}\right)\sqrt{\mathrm{4a}−\mathrm{1}}}\mathrm{arctan}\left(\frac{\mathrm{2}\sqrt{\mathrm{x}}+\mathrm{1}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}\right) \\ $$$$−\frac{\mathrm{2a}+\mathrm{1}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}×\frac{\left(\mathrm{2}\sqrt{\mathrm{x}}+\mathrm{1}\right)\left(−\frac{\mathrm{2}}{\left(\mathrm{4a}−\mathrm{1}\right)\sqrt{\mathrm{4a}−\mathrm{1}}}\right)}{\mathrm{1}+\left(\frac{\mathrm{2}\sqrt{\mathrm{x}}+\mathrm{1}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{x}+\sqrt{\mathrm{x}}+\mathrm{a}\right)}−\frac{\mathrm{4a}−\mathrm{4}}{\left(\mathrm{4a}−\mathrm{1}\right)\sqrt{\mathrm{4a}−\mathrm{1}}}\mathrm{arctan}\left(\frac{\mathrm{2}\sqrt{\mathrm{x}}+\mathrm{1}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}\right) \\ $$$$+\frac{\mathrm{2}\left(\mathrm{2a}+\mathrm{1}\right)\left(\mathrm{2}\sqrt{\mathrm{x}}+\mathrm{1}\right)}{\left(\mathrm{4a}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{1}+\left(\frac{\mathrm{2}\sqrt{\mathrm{x}}+\mathrm{1}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}\right)^{\mathrm{2}} \right)}\:\Rightarrow \\ $$$$−\mathrm{f}^{'} \left(\mathrm{1}\right)=−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{x}+\sqrt{\mathrm{x}}+\mathrm{1}\right)}\:+\frac{\mathrm{6}\left(\mathrm{2}\sqrt{\mathrm{x}}+\mathrm{1}\right)}{\mathrm{9}\left(\mathrm{1}+\left(\frac{\mathrm{2}\sqrt{\mathrm{x}}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} \right.}\:+\mathrm{K} \\ $$$$ \\ $$
