Question Number 79472 by jagoll last updated on 25/Jan/20

$$\mathrm{what}\:\mathrm{the}\:\mathrm{minimum}\:\mathrm{value}\:\mathrm{of} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{5}}\:+\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{14x}+\mathrm{65}} \\ $$
Commented by john santu last updated on 25/Jan/20
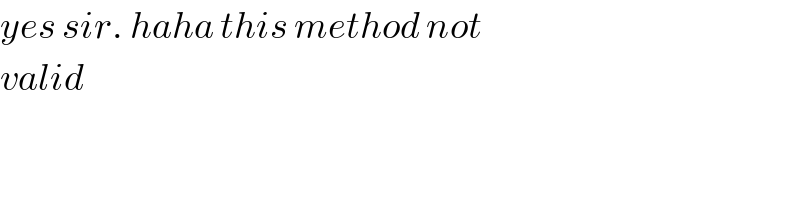
$${yes}\:{sir}.\:{haha}\:{this}\:{method}\:{not}\: \\ $$$${valid} \\ $$
Commented by mr W last updated on 25/Jan/20

$${f}={a}+{b}\:{with}\:{a},{b}>\mathrm{0} \\ $$$$“{f}_{{min}} \:{occurs}\:{when}\:{a}={b}''\:{is}\:{valid}\:{only}\:{if} \\ $$$${a}\:{and}\:{b}\:{are}\:{independent}\:{from}\:{each} \\ $$$${other}. \\ $$$${if}\:{a}\:{and}\:{b}\:{are}\:{dependent}\:{from}\:{each} \\ $$$${other},\:{such}\:{as}\:{in}\:{our}\:{case},\:{f}_{{min}} \:{occurs} \\ $$$${not}\:{always}\:{when}\:{a}={b}.\:\:\frac{{df}}{{dx}}=\frac{{da}}{{dx}}+\frac{{db}}{{dx}}=\mathrm{0} \\ $$$${doesn}'{t}\:{automatically}\:{lead}\:{to}\:{a}={b}. \\ $$
Commented by jagoll last updated on 25/Jan/20

Commented by jagoll last updated on 25/Jan/20
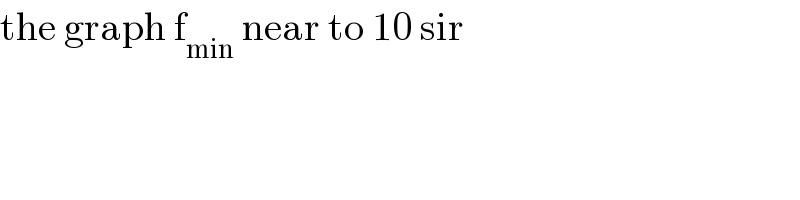
$$\mathrm{the}\:\mathrm{graph}\:\mathrm{f}_{\mathrm{min}} \:\mathrm{near}\:\mathrm{to}\:\mathrm{10}\:\mathrm{sir} \\ $$
Commented by jagoll last updated on 25/Jan/20

$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\mathrm{f}\left(\mathrm{x}\right)\:=\sqrt{\mathrm{8}}+\sqrt{\mathrm{52}}\:=\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{2}\sqrt{\mathrm{13}} \\ $$$$=\mathrm{10}.\mathrm{039} \\ $$
