Question Number 79644 by loveineq. last updated on 26/Jan/20
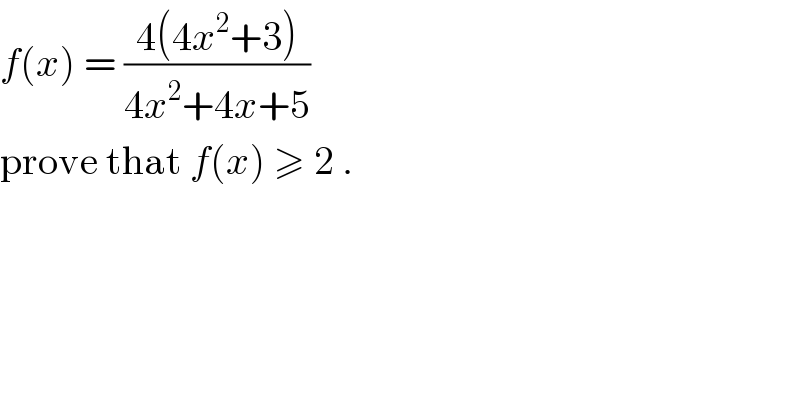
$${f}\left({x}\right)\:=\:\frac{\mathrm{4}\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{3}\right)}{\mathrm{4}{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{5}} \\ $$$$\mathrm{prove}\:\mathrm{that}\:{f}\left({x}\right)\:\geqslant\:\mathrm{2}\:. \\ $$
Commented by john santu last updated on 27/Jan/20

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)<\mathrm{2} \\ $$$$\frac{\mathrm{16x}^{\mathrm{2}} +\mathrm{12}}{\mathrm{4x}^{\mathrm{2}} +\mathrm{4x}+\mathrm{5}}<\mathrm{2}\:\Rightarrow\mathrm{4x}^{\mathrm{2}} +\mathrm{4x}+\mathrm{5}>\mathrm{0}\:\forall\mathrm{x}\in\mathbb{R} \\ $$$$\mathrm{16x}^{\mathrm{2}} +\mathrm{12}<\mathrm{8x}^{\mathrm{2}} +\mathrm{8x}+\mathrm{10} \\ $$$$\mathrm{8x}^{\mathrm{2}} −\mathrm{8x}+\mathrm{2}<\mathrm{0}\:\Rightarrow\Delta=\:\mathrm{64}−\mathrm{4}.\mathrm{8}.\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\frac{\mathrm{1}}{\mathrm{4}}=\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \geqslant\mathrm{0} \\ $$$$\mathrm{contradiction}\:\mathrm{with}\:\mathrm{the}\:\mathrm{initial} \\ $$$$\mathrm{statement}. \\ $$$$\mathrm{so}\:\mathrm{f}\left(\mathrm{x}\right)\geqslant\mathrm{2}. \\ $$$$ \\ $$
Answered by mr W last updated on 27/Jan/20
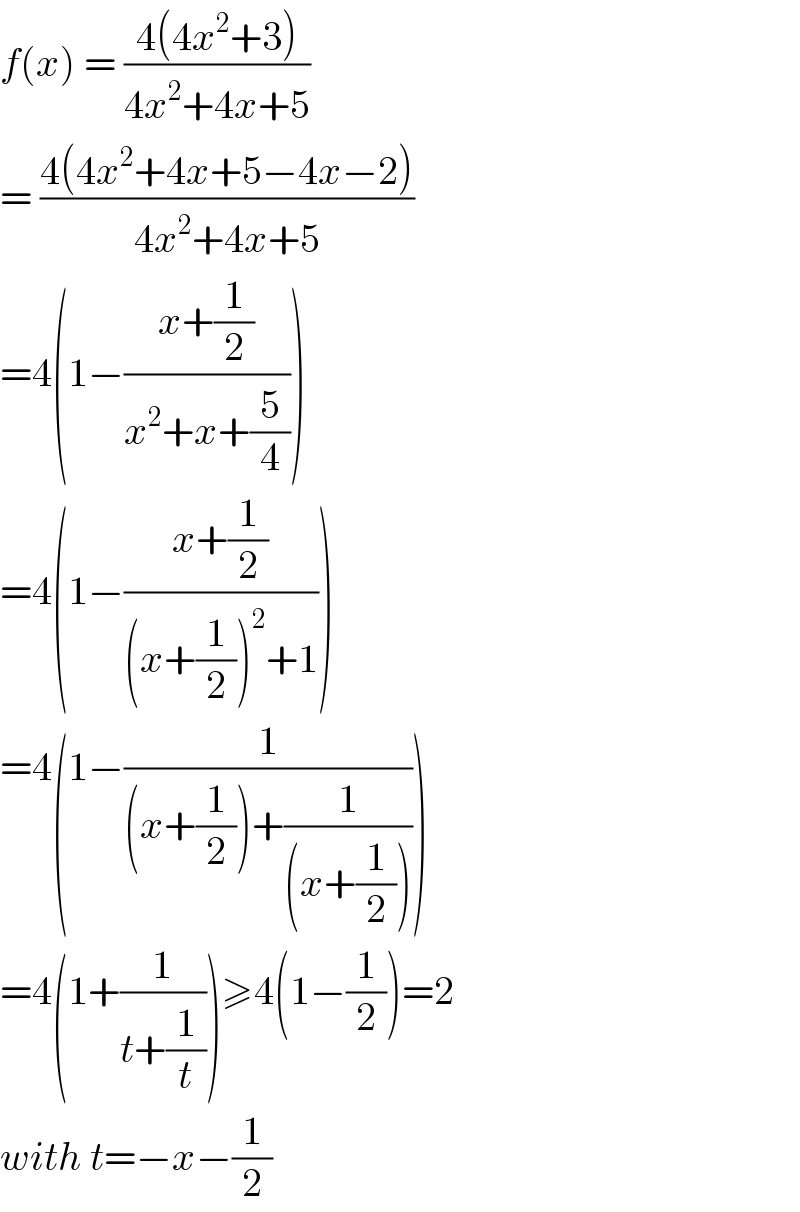
$${f}\left({x}\right)\:=\:\frac{\mathrm{4}\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{3}\right)}{\mathrm{4}{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{5}} \\ $$$$=\:\frac{\mathrm{4}\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{5}−\mathrm{4}{x}−\mathrm{2}\right)}{\mathrm{4}{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{5}} \\ $$$$=\mathrm{4}\left(\mathrm{1}−\frac{{x}+\frac{\mathrm{1}}{\mathrm{2}}}{{x}^{\mathrm{2}} +{x}+\frac{\mathrm{5}}{\mathrm{4}}}\right) \\ $$$$=\mathrm{4}\left(\mathrm{1}−\frac{{x}+\frac{\mathrm{1}}{\mathrm{2}}}{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{1}}\right) \\ $$$$=\mathrm{4}\left(\mathrm{1}−\frac{\mathrm{1}}{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)}}\right) \\ $$$$=\mathrm{4}\left(\mathrm{1}+\frac{\mathrm{1}}{{t}+\frac{\mathrm{1}}{{t}}}\right)\geqslant\mathrm{4}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{2} \\ $$$${with}\:{t}=−{x}−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
