Question Number 79751 by Rio Michael last updated on 27/Jan/20
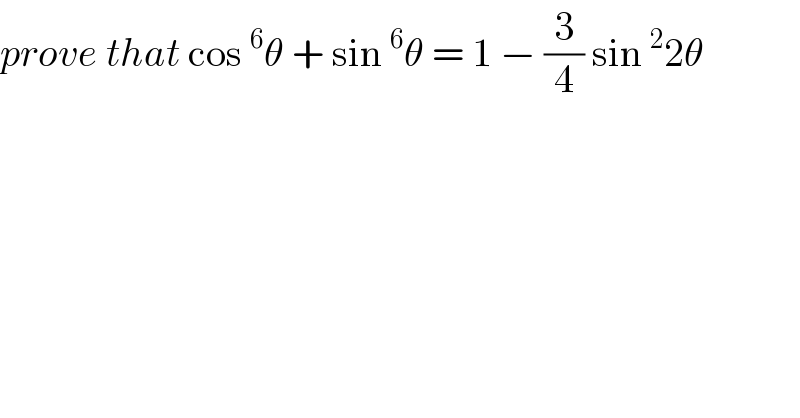
$${prove}\:{that}\:\mathrm{cos}\:^{\mathrm{6}} \theta\:+\:\mathrm{sin}\:^{\mathrm{6}} \theta\:=\:\mathrm{1}\:−\:\frac{\mathrm{3}}{\mathrm{4}}\:\mathrm{sin}\:^{\mathrm{2}} \mathrm{2}\theta \\ $$
Answered by mind is power last updated on 27/Jan/20
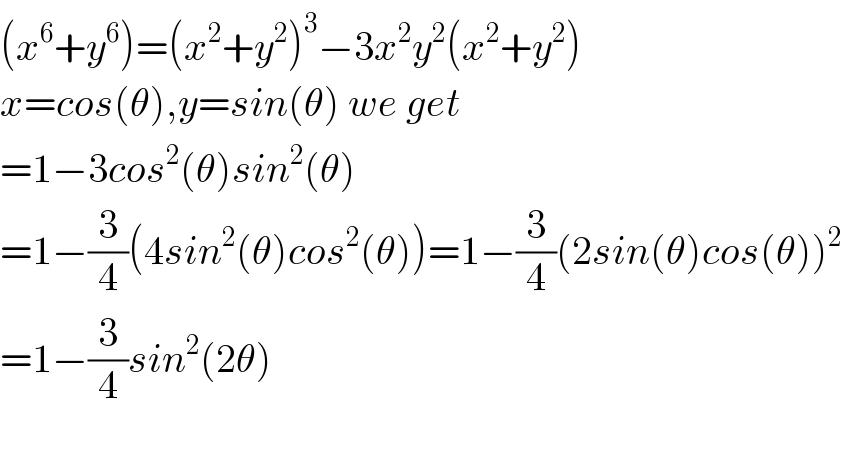
$$\left({x}^{\mathrm{6}} +{y}^{\mathrm{6}} \right)=\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} {y}^{\mathrm{2}} \left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right) \\ $$$${x}={cos}\left(\theta\right),{y}={sin}\left(\theta\right)\:{we}\:{get} \\ $$$$=\mathrm{1}−\mathrm{3}{cos}^{\mathrm{2}} \left(\theta\right){sin}^{\mathrm{2}} \left(\theta\right) \\ $$$$=\mathrm{1}−\frac{\mathrm{3}}{\mathrm{4}}\left(\mathrm{4}{sin}^{\mathrm{2}} \left(\theta\right){cos}^{\mathrm{2}} \left(\theta\right)\right)=\mathrm{1}−\frac{\mathrm{3}}{\mathrm{4}}\left(\mathrm{2}{sin}\left(\theta\right){cos}\left(\theta\right)\right)^{\mathrm{2}} \\ $$$$=\mathrm{1}−\frac{\mathrm{3}}{\mathrm{4}}{sin}^{\mathrm{2}} \left(\mathrm{2}\theta\right) \\ $$$$ \\ $$
Commented by Rio Michael last updated on 27/Jan/20

$${thanks} \\ $$
Answered by Henri Boucatchou last updated on 28/Jan/20
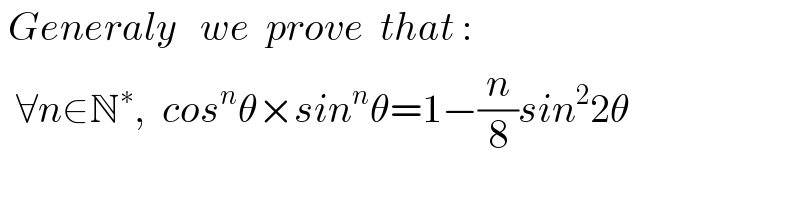
$$\:{Generaly}\:\:\:{we}\:\:{prove}\:\:{that}\:: \\ $$$$\:\:\forall{n}\in\mathbb{N}^{\ast} ,\:\:{cos}^{{n}} \theta×{sin}^{{n}} \theta=\mathrm{1}−\frac{{n}}{\mathrm{8}}{sin}^{\mathrm{2}} \mathrm{2}\theta \\ $$
