Question Number 79876 by mathocean1 last updated on 28/Jan/20
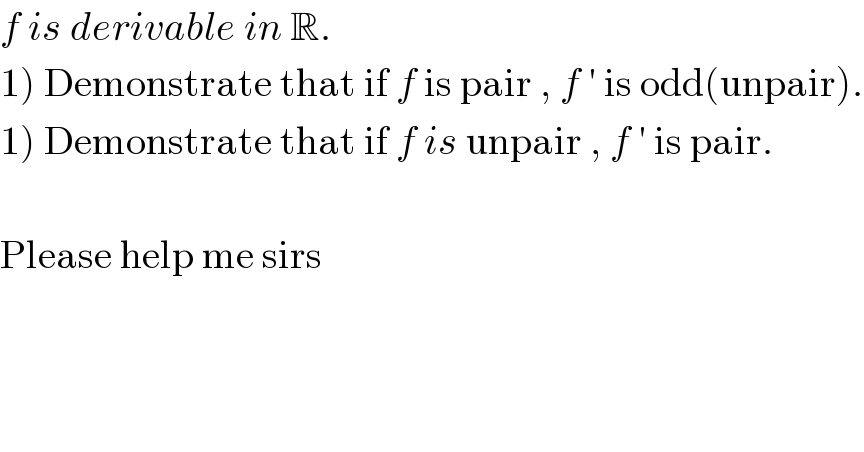
$${f}\:{is}\:{derivable}\:{in}\:\mathbb{R}. \\ $$$$\left.\mathrm{1}\right)\:\mathrm{Demonstrate}\:\mathrm{that}\:\mathrm{if}\:{f}\:\mathrm{is}\:\mathrm{pair}\:,\:{f}\:'\:\mathrm{is}\:\mathrm{odd}\left(\mathrm{unpair}\right). \\ $$$$\left.\mathrm{1}\right)\:\mathrm{Demonstrate}\:\mathrm{that}\:\mathrm{if}\:{f}\:{is}\:\mathrm{unpair}\:,\:{f}\:'\:\mathrm{is}\:\mathrm{pair}. \\ $$$$ \\ $$$$\mathrm{Please}\:\mathrm{help}\:\mathrm{me}\:\mathrm{sirs} \\ $$
Commented by MJS last updated on 29/Jan/20

$$\mathrm{if}\:“\mathrm{pair}''\:\mathrm{means}\:{f}\left(−{x}\right)={f}\left({x}\right) \\ $$$$\mathrm{and}\:“\mathrm{unpair}''\:\mathrm{means}\:{f}\left(−{x}\right)=−{f}\left({x}\right) \\ $$$$\mathrm{then}\:\mathrm{i}.\mathrm{e}. \\ $$$${y}=\mathrm{cos}\:{x}\:\mathrm{and}\:{y}={x}^{\mathrm{2}} ;\:{y}={x}^{\mathrm{4}} \:\mathrm{are}\:\mathrm{pair} \\ $$$${y}=\mathrm{sin}\:{x}\:\mathrm{and}\:{y}={x};\:{y}={x}^{\mathrm{3}} \:\mathrm{are}\:\mathrm{unpair} \\ $$$$\mathrm{draw}\:\mathrm{them}\:\mathrm{and}\:\mathrm{try}\:\mathrm{to}\:\mathrm{understand}\:\mathrm{how}\:\mathrm{the} \\ $$$$\mathrm{slopes}\:\mathrm{must}\:\mathrm{look}\:\mathrm{like} \\ $$
Answered by Henri Boucatchou last updated on 29/Jan/20
![f is derivable for all x_0 ∈R, that′s lim_(x→x_0 ) ((f(x)−f(x_0 ))/(x−x_0 ))=f ′(x_0 ) f pair ⇒ lim_(x−→x_0 ) −((f(−x)−f(−x_0 ))/((−x)−(−x_0 )))=−f ′(−x_0 )=lim_(x→x_0 ) ((f(x)−f(x_0 ))/(x−x_0 ))=f ′(x_0 ) ⇒ f ′(−x_0 )=−f ′(x_0 ) e.i. f ′ is odd; f unpair ⇒ lim_(x→x_0 ) −((f(−x)−f(−x_0 ))/((−x)−(−x_0 )))=−f ′(−x_0 )=lim_(x→x_0 ) ((−[f(x)−f(x_0 )])/(x−x_0 ))=−f ′(x_0 ) ⇒−f ′(−x_0 )=−f ′(x_0 ) ⇒ f ′(−x_0 )=f ′(x_0 ) e.i. f ′ is pair.](https://www.tinkutara.com/question/Q79912.png)
$$\:\:{f}\:\:{is}\:\:{derivable}\:\:{for}\:\:{all}\:{x}_{\mathrm{0}} \in\mathbb{R},\:\:{that}'{s} \\ $$$$\:\underset{{x}\rightarrow{x}_{\mathrm{0}} } {{lim}}\frac{{f}\left({x}\right)−{f}\left({x}_{\mathrm{0}} \right)}{{x}−{x}_{\mathrm{0}} }={f}\:'\left({x}_{\mathrm{0}} \right) \\ $$$${f}\:\:{pair}\:\:\Rightarrow\:\:\underset{{x}−\rightarrow{x}_{\mathrm{0}} } {{lim}}−\frac{{f}\left(−{x}\right)−{f}\left(−{x}_{\mathrm{0}} \right)}{\left(−{x}\right)−\left(−{x}_{\mathrm{0}} \right)}=−{f}\:'\left(−{x}_{\mathrm{0}} \right)=\underset{{x}\rightarrow{x}_{\mathrm{0}} } {{lim}}\frac{{f}\left({x}\right)−{f}\left({x}_{\mathrm{0}} \right)}{{x}−{x}_{\mathrm{0}} }={f}\:'\left({x}_{\mathrm{0}} \right) \\ $$$$\:\:\Rightarrow\:{f}\:'\left(−{x}_{\mathrm{0}} \right)=−{f}\:'\left({x}_{\mathrm{0}} \right)\:\:{e}.{i}.\:\:{f}\:'\:\:{is}\:\:{odd}; \\ $$$${f}\:\:{unpair}\:\:\Rightarrow\:\:\underset{{x}\rightarrow{x}_{\mathrm{0}} } {{lim}}−\frac{{f}\left(−{x}\right)−{f}\left(−{x}_{\mathrm{0}} \right)}{\left(−{x}\right)−\left(−{x}_{\mathrm{0}} \right)}=−{f}\:'\left(−{x}_{\mathrm{0}} \right)=\underset{{x}\rightarrow{x}_{\mathrm{0}} } {{lim}}\frac{−\left[{f}\left({x}\right)−{f}\left({x}_{\mathrm{0}} \right)\right]}{{x}−{x}_{\mathrm{0}} }=−{f}\:'\left({x}_{\mathrm{0}} \right) \\ $$$$\:\:\Rightarrow−{f}\:'\left(−{x}_{\mathrm{0}} \right)=−{f}\:'\left({x}_{\mathrm{0}} \right) \\ $$$$\:\:\Rightarrow\:\:{f}\:'\left(−{x}_{\mathrm{0}} \right)={f}\:'\left({x}_{\mathrm{0}} \right)\:\:{e}.{i}.\:\:{f}\:'\:\:{is}\:\:{pair}. \\ $$
