Menu Close

Question-79943

Tinku Tara 0 Comments
Pin




Question Number 79943 by TawaTawa last updated on 29/Jan/20
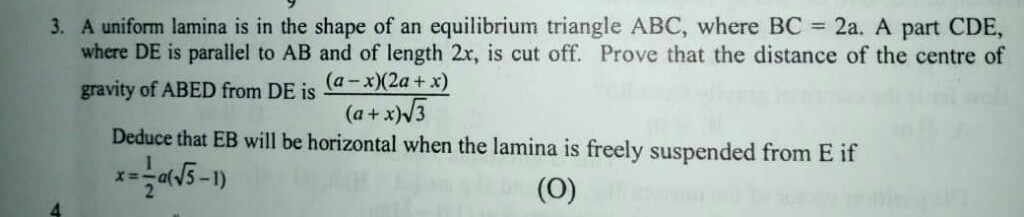
Commented by TawaTawa last updated on 29/Jan/20
Equilateral triangle not equilibrium triangle
$$\mathrm{Equilateral}\:\mathrm{triangle}\:\mathrm{not}\:\mathrm{equilibrium}\:\mathrm{triangle} \\ $$
Commented by TawaTawa last updated on 29/Jan/20
I cannot show it. the b part
$$\mathrm{I}\:\mathrm{cannot}\:\mathrm{show}\:\mathrm{it}.\:\mathrm{the}\:\mathrm{b}\:\mathrm{part} \\ $$
Commented by TawaTawa last updated on 29/Jan/20
Alright sir, help me please. God bless you sir.
$$\mathrm{Alright}\:\mathrm{sir},\:\:\mathrm{help}\:\mathrm{me}\:\mathrm{please}.\:\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by mr W last updated on 29/Jan/20
what′s your difficulty?
$${what}'{s}\:{your}\:{difficulty}? \\ $$
Commented by mr W last updated on 30/Jan/20
question has terribly some errors. i answered the question in the way how i think it should be. e.g. EB can never be horizontal. but EA can be horizontal.
$${question}\:{has}\:{terribly}\:{some}\:{errors}. \\ $$$${i}\:{answered}\:{the}\:{question}\:{in}\:{the}\:{way} \\ $$$${how}\:{i}\:{think}\:{it}\:{should}\:{be}.\:{e}.{g}.\:{EB} \\ $$$${can}\:{never}\:{be}\:{horizontal}.\:{but}\:{EA}\:{can} \\ $$$${be}\:{horizontal}. \\ $$
Answered by mr W last updated on 30/Jan/20
Commented by mr W last updated on 30/Jan/20
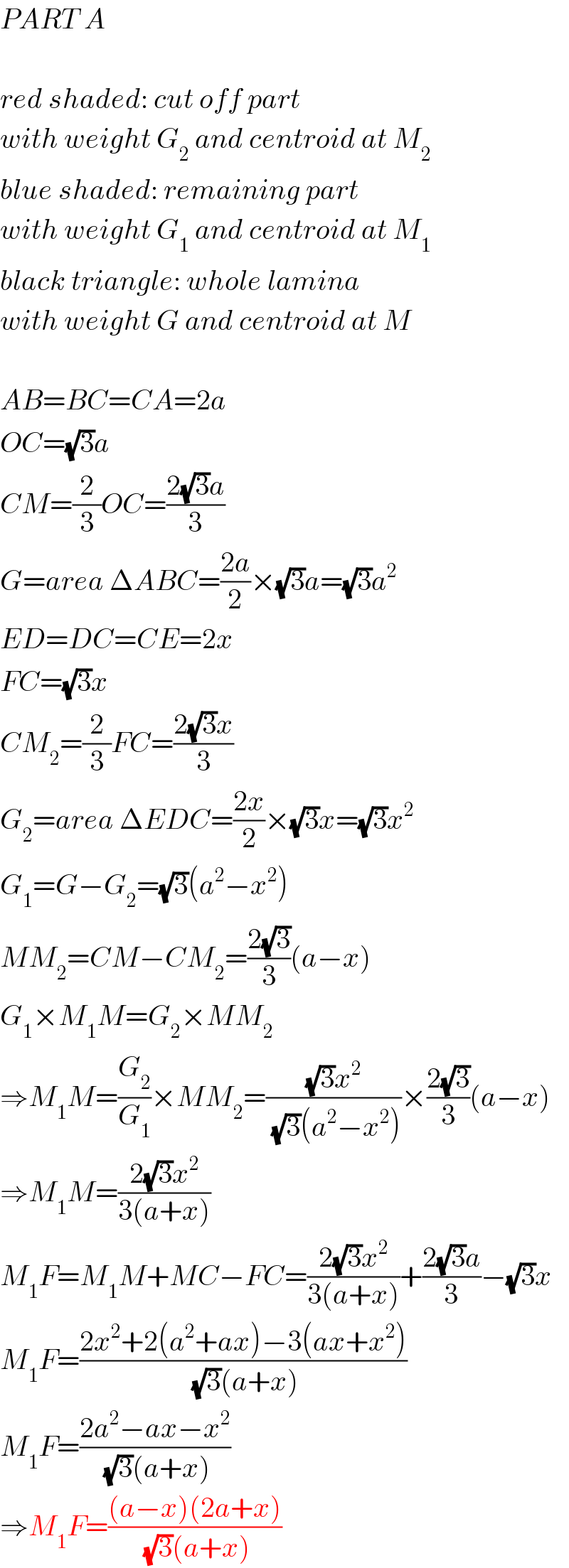
PART A red shaded: cut off part with weight G_2 and centroid at M_2 blue shaded: remaining part with weight G_1 and centroid at M_1 black triangle: whole lamina with weight G and centroid at M AB=BC=CA=2a OC=(√3)a CM=(2/3)OC=((2(√3)a)/3) G=area ΔABC=((2a)/2)×(√3)a=(√3)a^2 ED=DC=CE=2x FC=(√3)x CM_2 =(2/3)FC=((2(√3)x)/3) G_2 =area ΔEDC=((2x)/2)×(√3)x=(√3)x^2 G_1 =G−G_2 =(√3)(a^2 −x^2 ) MM_2 =CM−CM_2 =((2(√3))/3)(a−x) G_1 ×M_1 M=G_2 ×MM_2 ⇒M_1 M=(G_2 /G_1 )×MM_2 =(((√3)x^2 )/( (√3)(a^2 −x^2 )))×((2(√3))/3)(a−x) ⇒M_1 M=((2(√3)x^2 )/(3(a+x))) M_1 F=M_1 M+MC−FC=((2(√3)x^2 )/(3(a+x)))+((2(√3)a)/3)−(√3)x M_1 F=((2x^2 +2(a^2 +ax)−3(ax+x^2 ))/( (√3)(a+x))) M_1 F=((2a^2 −ax−x^2 )/( (√3)(a+x))) ⇒M_1 F=(((a−x)(2a+x))/( (√3)(a+x)))
$${PART}\:{A} \\ $$$$ \\ $$$${red}\:{shaded}:\:{cut}\:{off}\:{part} \\ $$$${with}\:{weight}\:{G}_{\mathrm{2}} \:{and}\:{centroid}\:{at}\:{M}_{\mathrm{2}} \\ $$$${blue}\:{shaded}:\:{remaining}\:{part} \\ $$$${with}\:{weight}\:{G}_{\mathrm{1}} \:{and}\:{centroid}\:{at}\:{M}_{\mathrm{1}} \\ $$$${black}\:{triangle}:\:{whole}\:{lamina} \\ $$$${with}\:{weight}\:{G}\:{and}\:{centroid}\:{at}\:{M} \\ $$$$ \\ $$$${AB}={BC}={CA}=\mathrm{2}{a} \\ $$$${OC}=\sqrt{\mathrm{3}}{a} \\ $$$${CM}=\frac{\mathrm{2}}{\mathrm{3}}{OC}=\frac{\mathrm{2}\sqrt{\mathrm{3}}{a}}{\mathrm{3}} \\ $$$${G}={area}\:\Delta{ABC}=\frac{\mathrm{2}{a}}{\mathrm{2}}×\sqrt{\mathrm{3}}{a}=\sqrt{\mathrm{3}}{a}^{\mathrm{2}} \\ $$$${ED}={DC}={CE}=\mathrm{2}{x} \\ $$$${FC}=\sqrt{\mathrm{3}}{x} \\ $$$${CM}_{\mathrm{2}} =\frac{\mathrm{2}}{\mathrm{3}}{FC}=\frac{\mathrm{2}\sqrt{\mathrm{3}}{x}}{\mathrm{3}} \\ $$$${G}_{\mathrm{2}} ={area}\:\Delta{EDC}=\frac{\mathrm{2}{x}}{\mathrm{2}}×\sqrt{\mathrm{3}}{x}=\sqrt{\mathrm{3}}{x}^{\mathrm{2}} \\ $$$${G}_{\mathrm{1}} ={G}−{G}_{\mathrm{2}} =\sqrt{\mathrm{3}}\left({a}^{\mathrm{2}} −{x}^{\mathrm{2}} \right) \\ $$$${MM}_{\mathrm{2}} ={CM}−{CM}_{\mathrm{2}} =\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\left({a}−{x}\right) \\ $$$${G}_{\mathrm{1}} ×{M}_{\mathrm{1}} {M}={G}_{\mathrm{2}} ×{MM}_{\mathrm{2}} \\ $$$$\Rightarrow{M}_{\mathrm{1}} {M}=\frac{{G}_{\mathrm{2}} }{{G}_{\mathrm{1}} }×{MM}_{\mathrm{2}} =\frac{\sqrt{\mathrm{3}}{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{3}}\left({a}^{\mathrm{2}} −{x}^{\mathrm{2}} \right)}×\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\left({a}−{x}\right) \\ $$$$\Rightarrow{M}_{\mathrm{1}} {M}=\frac{\mathrm{2}\sqrt{\mathrm{3}}{x}^{\mathrm{2}} }{\mathrm{3}\left({a}+{x}\right)} \\ $$$${M}_{\mathrm{1}} {F}={M}_{\mathrm{1}} {M}+{MC}−{FC}=\frac{\mathrm{2}\sqrt{\mathrm{3}}{x}^{\mathrm{2}} }{\mathrm{3}\left({a}+{x}\right)}+\frac{\mathrm{2}\sqrt{\mathrm{3}}{a}}{\mathrm{3}}−\sqrt{\mathrm{3}}{x} \\ $$$${M}_{\mathrm{1}} {F}=\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}\left({a}^{\mathrm{2}} +{ax}\right)−\mathrm{3}\left({ax}+{x}^{\mathrm{2}} \right)}{\:\sqrt{\mathrm{3}}\left({a}+{x}\right)} \\ $$$${M}_{\mathrm{1}} {F}=\frac{\mathrm{2}{a}^{\mathrm{2}} −{ax}−{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{3}}\left({a}+{x}\right)} \\ $$$$\Rightarrow{M}_{\mathrm{1}} {F}=\frac{\left({a}−{x}\right)\left(\mathrm{2}{a}+{x}\right)}{\:\sqrt{\mathrm{3}}\left({a}+{x}\right)} \\ $$
Commented by mr W last updated on 30/Jan/20
Commented by mr W last updated on 30/Jan/20
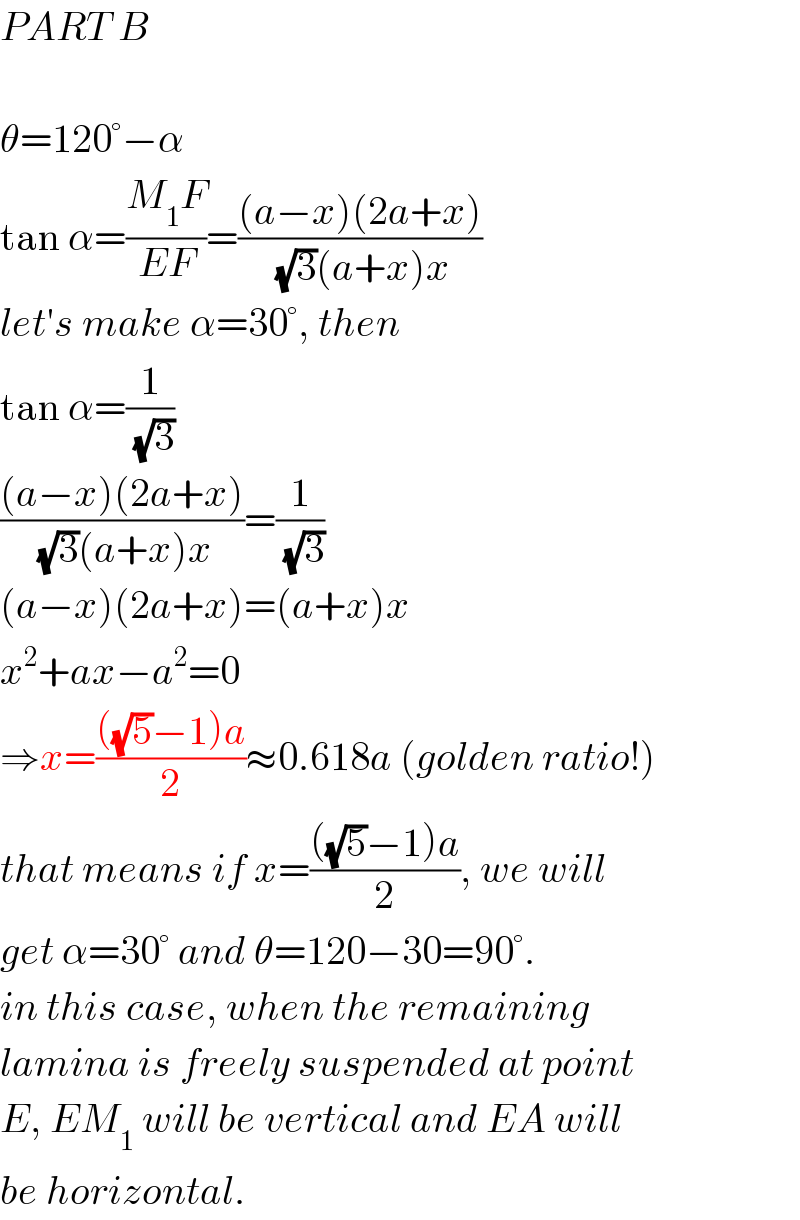
PART B θ=120°−α tan α=((M_1 F)/(EF))=(((a−x)(2a+x))/( (√3)(a+x)x)) let′s make α=30°, then tan α=(1/( (√3))) (((a−x)(2a+x))/( (√3)(a+x)x))=(1/( (√3))) (a−x)(2a+x)=(a+x)x x^2 +ax−a^2 =0 ⇒x=((((√5)−1)a)/2)≈0.618a (golden ratio!) that means if x=((((√5)−1)a)/2), we will get α=30° and θ=120−30=90°. in this case, when the remaining lamina is freely suspended at point E, EM_1 will be vertical and EA will be horizontal.
$${PART}\:{B} \\ $$$$ \\ $$$$\theta=\mathrm{120}°−\alpha \\ $$$$\mathrm{tan}\:\alpha=\frac{{M}_{\mathrm{1}} {F}}{{EF}}=\frac{\left({a}−{x}\right)\left(\mathrm{2}{a}+{x}\right)}{\:\sqrt{\mathrm{3}}\left({a}+{x}\right){x}} \\ $$$${let}'{s}\:{make}\:\alpha=\mathrm{30}°,\:{then} \\ $$$$\mathrm{tan}\:\alpha=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$$\frac{\left({a}−{x}\right)\left(\mathrm{2}{a}+{x}\right)}{\:\sqrt{\mathrm{3}}\left({a}+{x}\right){x}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$$\left({a}−{x}\right)\left(\mathrm{2}{a}+{x}\right)=\left({a}+{x}\right){x} \\ $$$${x}^{\mathrm{2}} +{ax}−{a}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{\left(\sqrt{\mathrm{5}}−\mathrm{1}\right){a}}{\mathrm{2}}\approx\mathrm{0}.\mathrm{618}{a}\:\left({golden}\:{ratio}!\right) \\ $$$${that}\:{means}\:{if}\:{x}=\frac{\left(\sqrt{\mathrm{5}}−\mathrm{1}\right){a}}{\mathrm{2}},\:{we}\:{will} \\ $$$${get}\:\alpha=\mathrm{30}°\:{and}\:\theta=\mathrm{120}−\mathrm{30}=\mathrm{90}°. \\ $$$${in}\:{this}\:{case},\:{when}\:{the}\:{remaining} \\ $$$${lamina}\:{is}\:{freely}\:{suspended}\:{at}\:{point} \\ $$$${E},\:{EM}_{\mathrm{1}} \:{will}\:{be}\:{vertical}\:{and}\:{EA}\:{will} \\ $$$${be}\:{horizontal}. \\ $$
Commented by mr W last updated on 30/Jan/20
Commented by TawaTawa last updated on 30/Jan/20
Wow, God bless you sir. I will study it and understand. Thanks for your time always.
$$\mathrm{Wow},\:\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$$$\mathrm{I}\:\mathrm{will}\:\mathrm{study}\:\mathrm{it}\:\mathrm{and}\:\mathrm{understand}. \\ $$$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}\:\mathrm{always}. \\ $$
Commented by mr W last updated on 30/Jan/20
Extra task: Prove without calculation that it is impossible that EB is vertical when ABDE is freely suspended from E, regardless how large the cut off part CDE is.
$${Extra}\:{task}: \\ $$$${Prove}\:{without}\:{calculation}\:{that}\:{it} \\ $$$${is}\:{impossible}\:{that}\:{EB}\:{is}\:{vertical} \\ $$$${when}\:{ABDE}\:{is}\:{freely}\:{suspended} \\ $$$${from}\:{E},\:{regardless}\:{how}\:{large}\:{the}\:{cut} \\ $$$${off}\:{part}\:{CDE}\:{is}. \\ $$
Commented by mr W last updated on 30/Jan/20
Commented by mr W last updated on 30/Jan/20
EXTRA TASK OF=symmetry axis S=midpoint of OF Since the part left from S is larger than the part right from S, the centroid M_1 must lie on the left side of S. On the other side, let N be the intersection point from EB and OF, since ED is smaller than AB, N must lie on the right side of S. that is to say, M_1 can never coincide with N. When ABDE is suspendet from point E, EM_1 will be vertical. Since M_1 can never lie on the line EB, it means that EB can never be vertical, when ABDE is suspended on point E.
$${EXTRA}\:{TASK} \\ $$$${OF}={symmetry}\:{axis} \\ $$$${S}={midpoint}\:{of}\:{OF} \\ $$$${Since}\:{the}\:{part}\:{left}\:{from}\:{S}\:{is}\:{larger} \\ $$$${than}\:{the}\:{part}\:{right}\:{from}\:{S},\:{the}\:{centroid} \\ $$$${M}_{\mathrm{1}} \:{must}\:{lie}\:{on}\:{the}\:{left}\:{side}\:{of}\:{S}. \\ $$$${On}\:{the}\:{other}\:{side},\:{let}\:{N}\:{be}\:{the} \\ $$$${intersection}\:{point}\:{from}\:{EB}\:{and}\:{OF}, \\ $$$${since}\:{ED}\:{is}\:{smaller}\:{than}\:{AB},\:{N}\:{must} \\ $$$${lie}\:{on}\:{the}\:{right}\:{side}\:{of}\:{S}. \\ $$$${that}\:{is}\:{to}\:{say},\:{M}_{\mathrm{1}} \:{can}\:{never}\:{coincide} \\ $$$${with}\:{N}. \\ $$$${When}\:{ABDE}\:{is}\:{suspendet}\:{from}\:{point} \\ $$$${E},\:{EM}_{\mathrm{1}} \:{will}\:{be}\:{vertical}.\:{Since}\:{M}_{\mathrm{1}} \\ $$$${can}\:{never}\:{lie}\:{on}\:{the}\:{line}\:{EB},\:{it}\:{means} \\ $$$${that}\:{EB}\:{can}\:{never}\:{be}\:{vertical},\:{when} \\ $$$${ABDE}\:{is}\:{suspended}\:{on}\:{point}\:{E}. \\ $$
Commented by mr W last updated on 30/Jan/20
Commented by TawaTawa last updated on 30/Jan/20
I really appreciate your effort sir. Am preparing for the exam. God bless you more sir. you helped me alot.
$$\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{effort}\:\mathrm{sir}. \\ $$$$\mathrm{Am}\:\mathrm{preparing}\:\mathrm{for}\:\mathrm{the}\:\mathrm{exam}.\:\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{more}\:\mathrm{sir}. \\ $$$$\mathrm{you}\:\mathrm{helped}\:\mathrm{me}\:\mathrm{alot}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *