Menu Close

Question-14467

Tinku Tara 0 Comments
Pin




Question Number 14467 by Tinkutara last updated on 01/Jun/17
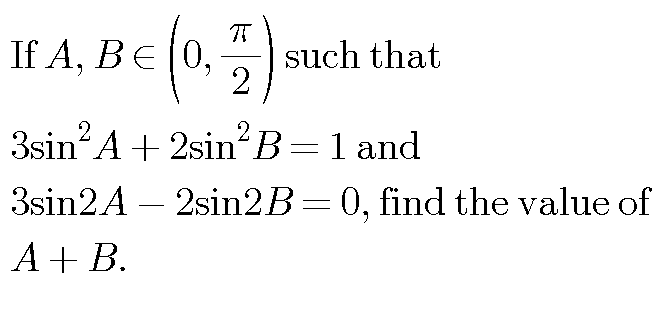
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 01/Jun/17
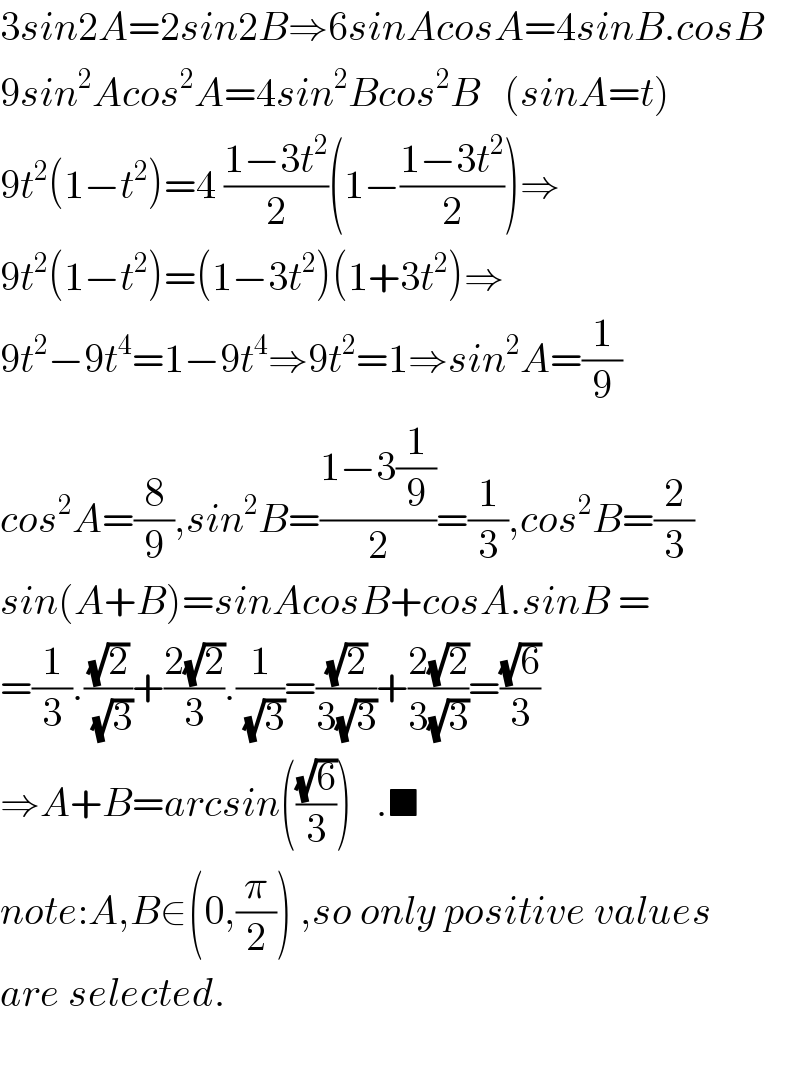
3sin2A=2sin2B⇒6sinAcosA=4sinB.cosB 9sin^2 Acos^2 A=4sin^2 Bcos^2 B (sinA=t) 9t^2 (1−t^2 )=4 ((1−3t^2 )/2)(1−((1−3t^2 )/2))⇒ 9t^2 (1−t^2 )=(1−3t^2 )(1+3t^2 )⇒ 9t^2 −9t^4 =1−9t^4 ⇒9t^2 =1⇒sin^2 A=(1/9) cos^2 A=(8/9),sin^2 B=((1−3(1/9))/2)=(1/3),cos^2 B=(2/3) sin(A+B)=sinAcosB+cosA.sinB = =(1/3).((√2)/( (√3)))+((2(√2))/3).(1/( (√3)))=((√2)/(3(√3)))+((2(√2))/(3(√3)))=((√6)/3) ⇒A+B=arcsin(((√6)/3)) .■ note:A,B∈(0,(π/2)) ,so only positive values are selected.
$$\mathrm{3}{sin}\mathrm{2}{A}=\mathrm{2}{sin}\mathrm{2}{B}\Rightarrow\mathrm{6}{sinAcosA}=\mathrm{4}{sinB}.{cosB} \\ $$$$\mathrm{9}{sin}^{\mathrm{2}} {Acos}^{\mathrm{2}} {A}=\mathrm{4}{sin}^{\mathrm{2}} {Bcos}^{\mathrm{2}} {B}\:\:\:\left({sinA}={t}\right) \\ $$$$\mathrm{9}{t}^{\mathrm{2}} \left(\mathrm{1}−{t}^{\mathrm{2}} \right)=\mathrm{4}\:\frac{\mathrm{1}−\mathrm{3}{t}^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}−\mathrm{3}{t}^{\mathrm{2}} }{\mathrm{2}}\right)\Rightarrow \\ $$$$\mathrm{9}{t}^{\mathrm{2}} \left(\mathrm{1}−{t}^{\mathrm{2}} \right)=\left(\mathrm{1}−\mathrm{3}{t}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{3}{t}^{\mathrm{2}} \right)\Rightarrow \\ $$$$\mathrm{9}{t}^{\mathrm{2}} −\mathrm{9}{t}^{\mathrm{4}} =\mathrm{1}−\mathrm{9}{t}^{\mathrm{4}} \Rightarrow\mathrm{9}{t}^{\mathrm{2}} =\mathrm{1}\Rightarrow{sin}^{\mathrm{2}} {A}=\frac{\mathrm{1}}{\mathrm{9}} \\ $$$${cos}^{\mathrm{2}} {A}=\frac{\mathrm{8}}{\mathrm{9}},{sin}^{\mathrm{2}} {B}=\frac{\mathrm{1}−\mathrm{3}\frac{\mathrm{1}}{\mathrm{9}}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{3}},{cos}^{\mathrm{2}} {B}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$${sin}\left({A}+{B}\right)={sinAcosB}+{cosA}.{sinB}\:= \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}.\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{3}}}+\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}.\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}=\frac{\sqrt{\mathrm{2}}}{\mathrm{3}\sqrt{\mathrm{3}}}+\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}\sqrt{\mathrm{3}}}=\frac{\sqrt{\mathrm{6}}}{\mathrm{3}} \\ $$$$\Rightarrow{A}+{B}={arcsin}\left(\frac{\sqrt{\mathrm{6}}}{\mathrm{3}}\right)\:\:\:.\blacksquare \\ $$$${note}:{A},{B}\in\left(\mathrm{0},\frac{\pi}{\mathrm{2}}\right)\:,{so}\:{only}\:{positive}\:{values} \\ $$$${are}\:{selected}. \\ $$$$ \\ $$
Commented by Tinkutara last updated on 01/Jun/17
Thanks Sir!
$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
Commented by myintkhaing last updated on 01/Jun/17
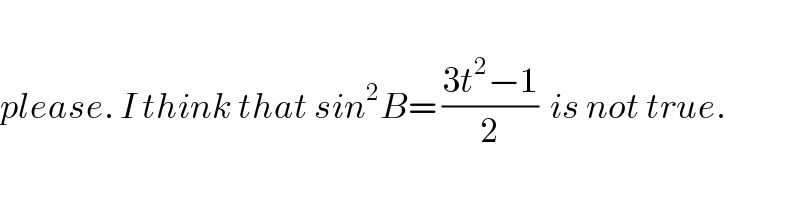
please. I think that sin^2 B= ((3t^2 −1)/2) is not true.
$$ \\ $$$${please}.\:{I}\:{think}\:{that}\:{sin}^{\mathrm{2}} {B}=\:\frac{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}}\:\:{is}\:{not}\:{true}. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 01/Jun/17
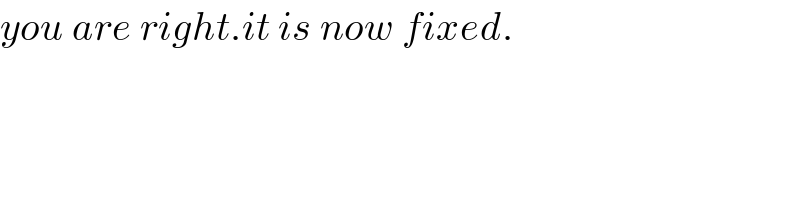
you are right.it is now fixed.
$${you}\:{are}\:{right}.{it}\:{is}\:{now}\:{fixed}. \\ $$
Commented by myintkhaing last updated on 02/Jun/17
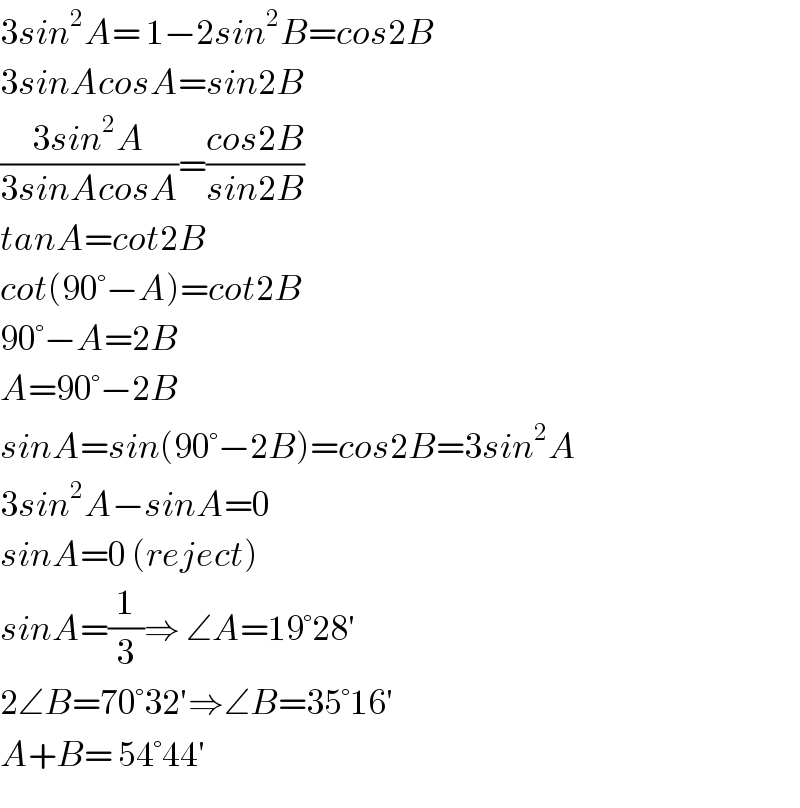
3sin^2 A= 1−2sin^2 B=cos2B 3sinAcosA=sin2B ((3sin^2 A)/(3sinAcosA))=((cos2B)/(sin2B)) tanA=cot2B cot(90°−A)=cot2B 90°−A=2B A=90°−2B sinA=sin(90°−2B)=cos2B=3sin^2 A 3sin^2 A−sinA=0 sinA=0 (reject) sinA=(1/3)⇒ ∠A=19°28′ 2∠B=70°32′⇒∠B=35°16′ A+B= 54°44′
$$\mathrm{3}{sin}^{\mathrm{2}} {A}=\:\mathrm{1}−\mathrm{2}{sin}^{\mathrm{2}} {B}={cos}\mathrm{2}{B} \\ $$$$\mathrm{3}{sinAcosA}={sin}\mathrm{2}{B} \\ $$$$\frac{\mathrm{3}{sin}^{\mathrm{2}} {A}}{\mathrm{3}{sinAcosA}}=\frac{{cos}\mathrm{2}{B}}{{sin}\mathrm{2}{B}} \\ $$$${tanA}={cot}\mathrm{2}{B} \\ $$$${cot}\left(\mathrm{90}°−{A}\right)={cot}\mathrm{2}{B} \\ $$$$\mathrm{90}°−{A}=\mathrm{2}{B} \\ $$$${A}=\mathrm{90}°−\mathrm{2}{B} \\ $$$${sinA}={sin}\left(\mathrm{90}°−\mathrm{2}{B}\right)={cos}\mathrm{2}{B}=\mathrm{3}{sin}^{\mathrm{2}} {A} \\ $$$$\mathrm{3}{sin}^{\mathrm{2}} {A}−{sinA}=\mathrm{0} \\ $$$${sinA}=\mathrm{0}\:\left({reject}\right) \\ $$$${sinA}=\frac{\mathrm{1}}{\mathrm{3}}\Rightarrow\:\angle{A}=\mathrm{19}°\mathrm{28}' \\ $$$$\mathrm{2}\angle{B}=\mathrm{70}°\mathrm{32}'\Rightarrow\angle{B}=\mathrm{35}°\mathrm{16}' \\ $$$${A}+{B}=\:\mathrm{54}°\mathrm{44}' \\ $$
Commented by Tinkutara last updated on 02/Jun/17
Thanks Sir!
$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *