Question Number 80093 by TawaTawa last updated on 30/Jan/20
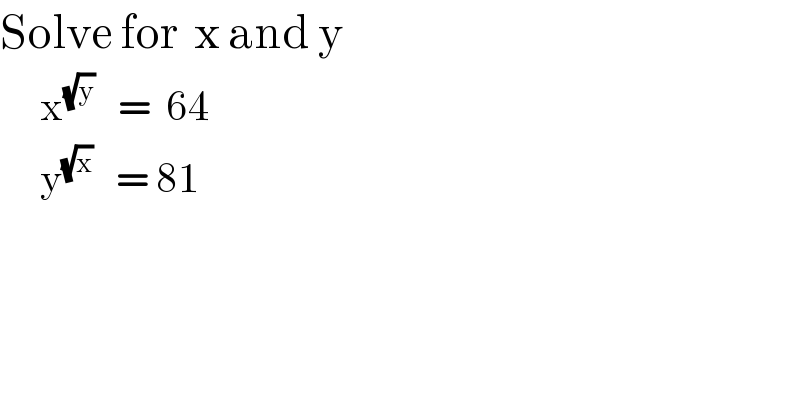
$$\mathrm{Solve}\:\mathrm{for}\:\:\mathrm{x}\:\mathrm{and}\:\mathrm{y} \\ $$$$\:\:\:\:\:\mathrm{x}^{\sqrt{\mathrm{y}}} \:\:\:=\:\:\mathrm{64} \\ $$$$\:\:\:\:\:\mathrm{y}^{\sqrt{\mathrm{x}}} \:\:\:=\:\mathrm{81} \\ $$
Answered by MJS last updated on 30/Jan/20

$$\mathrm{open}\:\mathrm{your}\:\mathrm{eyes}\:\mathrm{and}\:\mathrm{your}\:\mathrm{mind},\:\mathrm{this}\:\mathrm{is}\:\mathrm{super} \\ $$$$\mathrm{obvious}: \\ $$$$\mathrm{64}=\mathrm{4}^{\mathrm{3}} =\mathrm{4}^{\sqrt{\mathrm{9}}} \\ $$$$\mathrm{81}=\mathrm{9}^{\mathrm{2}} =\mathrm{9}^{\sqrt{\mathrm{4}}} \\ $$$${x}=\mathrm{4}\wedge{y}=\mathrm{9} \\ $$
Commented by TawaTawa last updated on 30/Jan/20

$$\mathrm{Hahahaha} \\ $$
Answered by john santu last updated on 30/Jan/20
![x > 0 , y > 0 [((√x))^2 ]^(√y) = [((√4))^2 ]^(√9) ∧ [((√y))^2 ]^(√x) = [((√9))^2 ]^(√4) ⇒x = 4 ∧ y=9](https://www.tinkutara.com/question/Q80099.png)
$$\mathrm{x}\:>\:\mathrm{0}\:,\:\mathrm{y}\:>\:\mathrm{0} \\ $$$$\left[\left(\sqrt{\mathrm{x}}\right)^{\mathrm{2}} \right]^{\sqrt{\mathrm{y}}} =\:\left[\left(\sqrt{\mathrm{4}}\right)^{\mathrm{2}} \right]^{\sqrt{\mathrm{9}}} \:\wedge\:\left[\left(\sqrt{\mathrm{y}}\right)^{\mathrm{2}} \right]^{\sqrt{\mathrm{x}}} =\:\left[\left(\sqrt{\mathrm{9}}\right)^{\mathrm{2}} \right]^{\sqrt{\mathrm{4}}} \\ $$$$\Rightarrow\mathrm{x}\:=\:\mathrm{4}\:\wedge\:\mathrm{y}=\mathrm{9} \\ $$
Commented by john santu last updated on 30/Jan/20
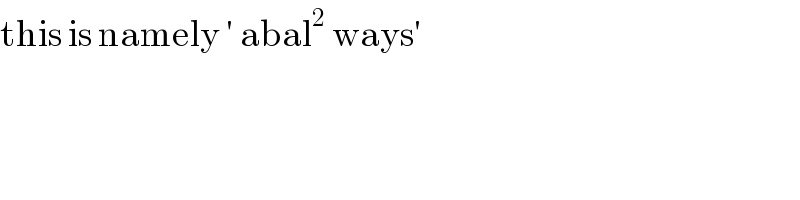
$$\mathrm{this}\:\mathrm{is}\:\mathrm{namely}\:'\:\mathrm{abal}^{\mathrm{2}} \:\mathrm{ways}' \\ $$
Commented by Joel578 last updated on 31/Jan/20

$$\mathrm{Sir}\:\mathrm{John}\:\mathrm{Santu}\:\mathrm{from}\:\mathrm{Indonesia}? \\ $$
Answered by Kamel Kamel last updated on 31/Jan/20
![Solve the system: { ((x^(√y) =64)),((y^(√x) =81)) :} Put: u=(√x),v=(√y) ∴ { ((u^(2v) =64)),((v^(2u) =81)) :}⇒ { ((vLn(u)=3Ln(2))),((uLn(v)=2Ln(3))) :} (u,v)=(2,3) particular solution. uLn(((Ln(8))/(Ln(u))))=Ln(9) and vLn(((Ln(9))/(Ln(v))))=Ln(8) ((Ln(8))/(Ln(u)))=9^(1/u) ⇒Ln(8)=9^(1/u) Ln(u) ( (((Ln(9))/(Ln(v))))=8^(1/v) ) ∴ Ln(8)=^(z=(1/u)) −9^z Ln(z) (and Ln(9)=−8^w Ln(w)where w=(1/v)) f(z)=−Ln(z)9^z ⇒f′(z)=−(((1+zLn(9))/z))9^z /z>0. f′(z)=0⇒z=−(1/(Ln(9))) f↘ ∀z∈]0;+∞[. f is a continous function. We have f((1/2))=Ln(8) then z=(1/2) is a unique solution. So x=u^2 =(1/z^2 )=4. With the same way we get: w=(1/3)⇒y=v^2 =(1/w^2 )=9. ∴ S={(4,9)}. KAMEL BENAICHA](https://www.tinkutara.com/question/Q80132.png)
$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{system}:\begin{cases}{\mathrm{x}^{\sqrt{\mathrm{y}}} =\mathrm{64}}\\{\mathrm{y}^{\sqrt{\mathrm{x}}} =\mathrm{81}}\end{cases} \\ $$$$\mathrm{Put}:\:{u}=\sqrt{{x}},{v}=\sqrt{{y}} \\ $$$$\therefore\:\begin{cases}{{u}^{\mathrm{2}{v}} =\mathrm{64}}\\{{v}^{\mathrm{2}{u}} =\mathrm{81}}\end{cases}\Rightarrow\begin{cases}{{v}\mathrm{Ln}\left({u}\right)=\mathrm{3Ln}\left(\mathrm{2}\right)}\\{{u}\mathrm{Ln}\left({v}\right)=\mathrm{2Ln}\left(\mathrm{3}\right)}\end{cases} \\ $$$$\left({u},{v}\right)=\left(\mathrm{2},\mathrm{3}\right)\:\mathrm{particular}\:\mathrm{solution}. \\ $$$${u}\mathrm{Ln}\left(\frac{\mathrm{Ln}\left(\mathrm{8}\right)}{\mathrm{Ln}\left({u}\right)}\right)=\mathrm{Ln}\left(\mathrm{9}\right)\:\mathrm{and}\:{v}\mathrm{Ln}\left(\frac{\mathrm{Ln}\left(\mathrm{9}\right)}{\mathrm{Ln}\left({v}\right)}\right)=\mathrm{Ln}\left(\mathrm{8}\right) \\ $$$$\frac{\mathrm{Ln}\left(\mathrm{8}\right)}{\mathrm{Ln}\left({u}\right)}=\mathrm{9}^{\frac{\mathrm{1}}{{u}}} \Rightarrow\mathrm{Ln}\left(\mathrm{8}\right)=\mathrm{9}^{\frac{\mathrm{1}}{{u}}} \mathrm{Ln}\left({u}\right)\:\left(\:\left(\frac{\mathrm{Ln}\left(\mathrm{9}\right)}{\mathrm{Ln}\left({v}\right)}\right)=\mathrm{8}^{\frac{\mathrm{1}}{{v}}} \right) \\ $$$$\therefore\:\mathrm{Ln}\left(\mathrm{8}\right)\overset{{z}=\frac{\mathrm{1}}{{u}}} {=}−\mathrm{9}^{{z}} \mathrm{Ln}\left({z}\right)\:\left(\mathrm{and}\:\mathrm{Ln}\left(\mathrm{9}\right)=−\mathrm{8}^{{w}} \mathrm{Ln}\left({w}\right)\mathrm{where}\:{w}=\frac{\mathrm{1}}{{v}}\right) \\ $$$${f}\left({z}\right)=−\mathrm{Ln}\left({z}\right)\mathrm{9}^{{z}} \Rightarrow{f}'\left({z}\right)=−\left(\frac{\mathrm{1}+{z}\mathrm{Ln}\left(\mathrm{9}\right)}{{z}}\right)\mathrm{9}^{{z}} \:/{z}>\mathrm{0}. \\ $$$${f}'\left({z}\right)=\mathrm{0}\Rightarrow{z}=−\frac{\mathrm{1}}{\mathrm{Ln}\left(\mathrm{9}\right)} \\ $$$$\left.{f}\searrow\:\forall{z}\in\right]\mathrm{0};+\infty\left[.\right. \\ $$$$\mathrm{f}\:\mathrm{is}\:\mathrm{a}\:\mathrm{continous}\:\mathrm{function}. \\ $$$$\mathrm{We}\:\mathrm{have}\:{f}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{Ln}\left(\mathrm{8}\right)\:\mathrm{then}\:{z}=\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{is}\:\mathrm{a}\:\mathrm{unique}\:\mathrm{solution}. \\ $$$$\mathrm{So}\:{x}={u}^{\mathrm{2}} =\frac{\mathrm{1}}{{z}^{\mathrm{2}} }=\mathrm{4}. \\ $$$$\mathrm{With}\:\mathrm{the}\:\mathrm{same}\:\mathrm{way}\:\mathrm{we}\:\mathrm{get}:\:\:{w}=\frac{\mathrm{1}}{\mathrm{3}}\Rightarrow{y}={v}^{\mathrm{2}} =\frac{\mathrm{1}}{{w}^{\mathrm{2}} }=\mathrm{9}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\therefore\:\:\:{S}=\left\{\left(\mathrm{4},\mathrm{9}\right)\right\}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{K}\mathrm{AMEL}}\:\boldsymbol{\mathrm{BENAICHA}} \\ $$
Commented by TawaTawa last updated on 31/Jan/20
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
