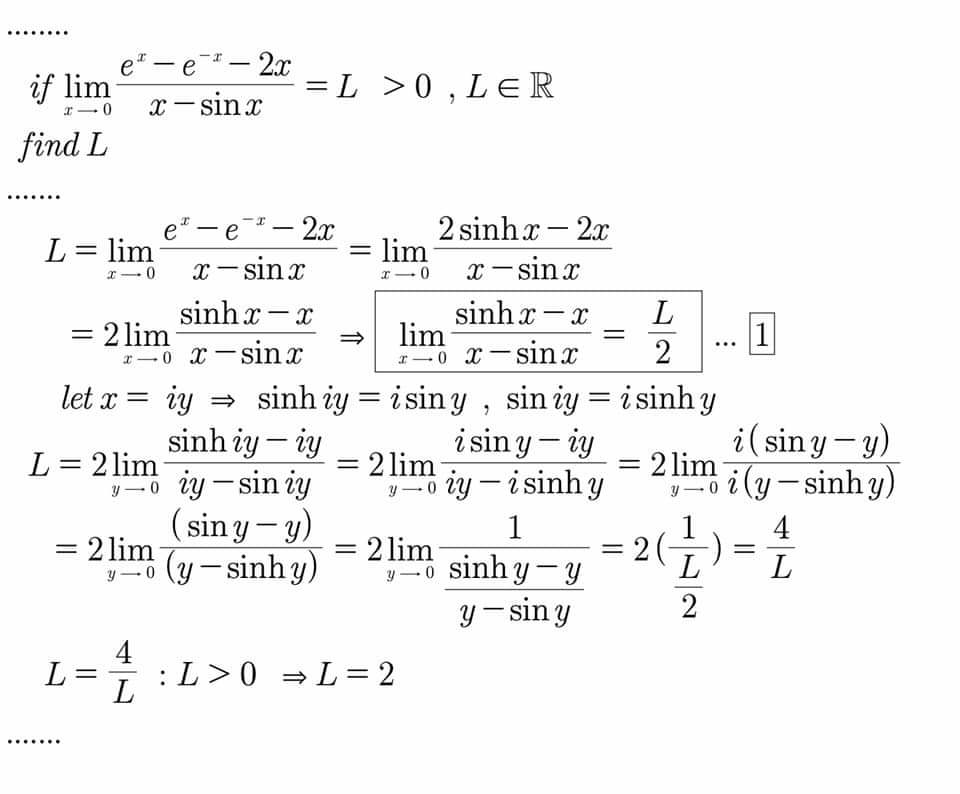lim-x-0-e-x-e-x-2x-x-sin-x-L-gt-0-L-R-find-L-with-out-using-hopital-and-Taylor-methods-

Tinku Tara June 4, 2023 Limits 0 Comments

Question Number 80276 by M±th+et£s last updated on 01/Feb/20

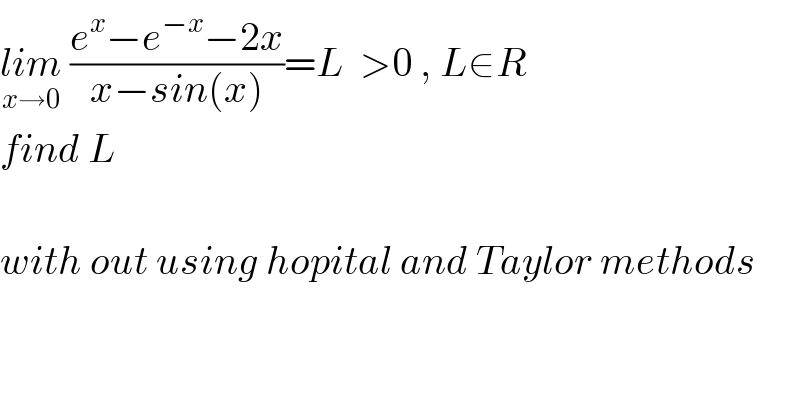
lim_(x→0) ((e^x −e^(−x) −2x)/(x−sin(x)))=L >0 , L∈R find L with out using hopital and Taylor methods

$$\underset{{x}\rightarrow\mathrm{0}} {{lim}}\:\frac{{e}^{{x}} −{e}^{−{x}} −\mathrm{2}{x}}{{x}−{sin}\left({x}\right)}={L}\:\:>\mathrm{0}\:,\:{L}\in{R} \\ $$$${find}\:{L} \\ $$$$ \\ $$$${with}\:{out}\:{using}\:{hopital}\:{and}\:{Taylor}\:{methods} \\ $$

Commented by mathmax by abdo last updated on 01/Feb/20

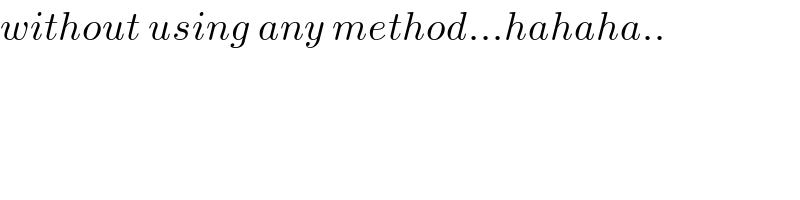
$${without}\:{using}\:{any}\:{method}…{hahaha}.. \\ $$

Answered by M±th+et£s last updated on 02/Feb/20

Facebook Tweet Pin

lim-x-0-e-x-e-x-2x-x-sin-x-L-gt-0-L-R-find-L-with-out-using-hopital-and-Taylor-methods-

Leave a Reply Cancel reply