Question Number 80343 by jagoll last updated on 02/Feb/20
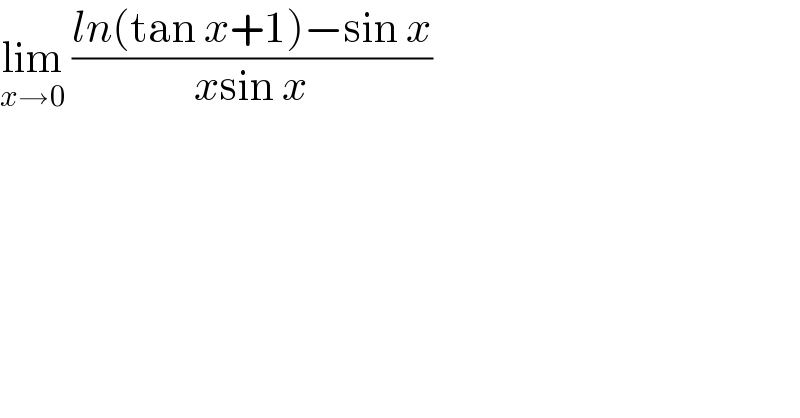
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{ln}\left(\mathrm{tan}\:{x}+\mathrm{1}\right)−\mathrm{sin}\:{x}}{{x}\mathrm{sin}\:{x}} \\ $$
Commented by abdomathmax last updated on 02/Feb/20
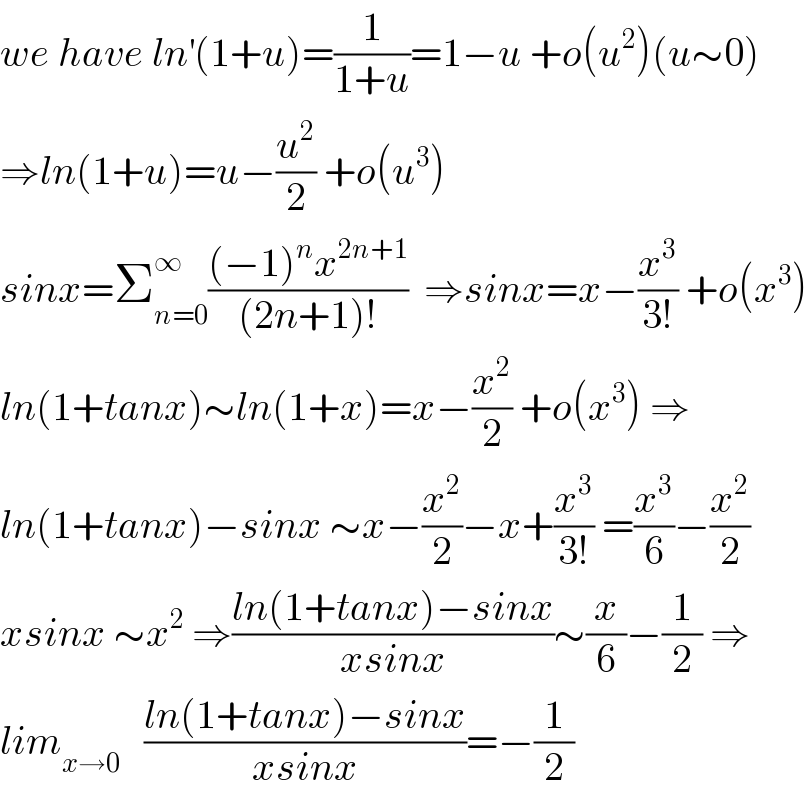
$${we}\:{have}\:{ln}^{'} \left(\mathrm{1}+{u}\right)=\frac{\mathrm{1}}{\mathrm{1}+{u}}=\mathrm{1}−{u}\:+{o}\left({u}^{\mathrm{2}} \right)\left({u}\sim\mathrm{0}\right) \\ $$$$\Rightarrow{ln}\left(\mathrm{1}+{u}\right)={u}−\frac{{u}^{\mathrm{2}} }{\mathrm{2}}\:+{o}\left({u}^{\mathrm{3}} \right) \\ $$$${sinx}=\sum_{{n}=\mathrm{0}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{2}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}\:\:\Rightarrow{sinx}={x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}\:+{o}\left({x}^{\mathrm{3}} \right) \\ $$$${ln}\left(\mathrm{1}+{tanx}\right)\sim{ln}\left(\mathrm{1}+{x}\right)={x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:+{o}\left({x}^{\mathrm{3}} \right)\:\Rightarrow \\ $$$${ln}\left(\mathrm{1}+{tanx}\right)−{sinx}\:\sim{x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}−{x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}\:=\frac{{x}^{\mathrm{3}} }{\mathrm{6}}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${xsinx}\:\sim{x}^{\mathrm{2}} \:\Rightarrow\frac{{ln}\left(\mathrm{1}+{tanx}\right)−{sinx}}{{xsinx}}\sim\frac{{x}}{\mathrm{6}}−\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\frac{{ln}\left(\mathrm{1}+{tanx}\right)−{sinx}}{{xsinx}}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by john santu last updated on 02/Feb/20
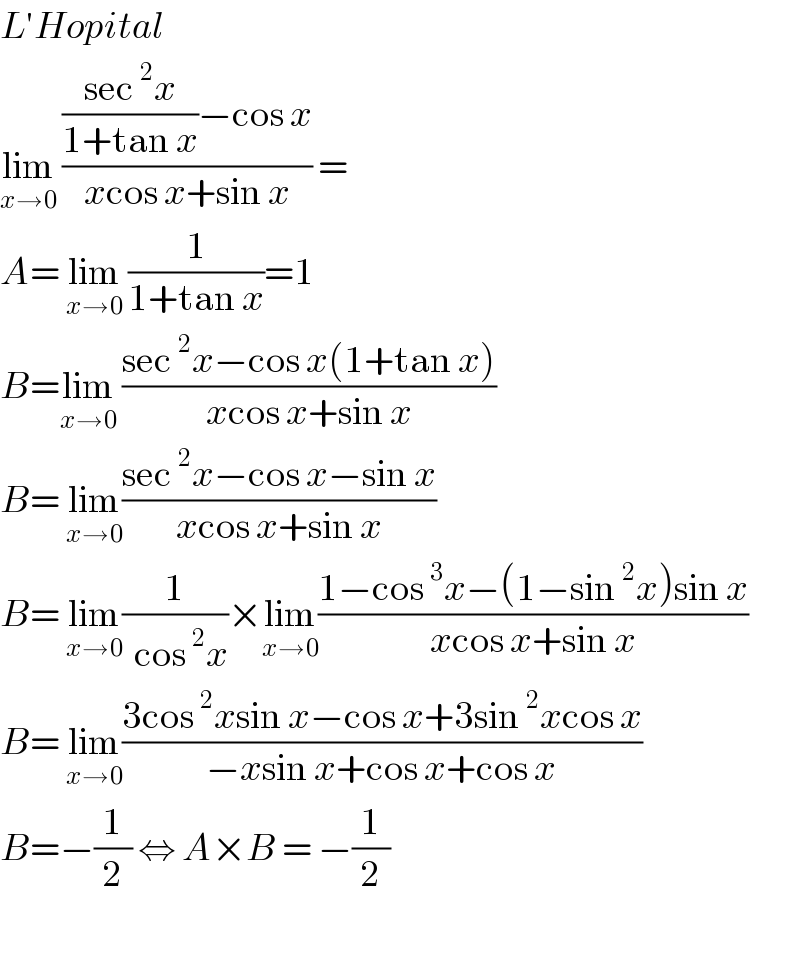
$${L}'{Hopital} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\mathrm{sec}\:^{\mathrm{2}} {x}}{\mathrm{1}+\mathrm{tan}\:{x}}−\mathrm{cos}\:{x}}{{x}\mathrm{cos}\:{x}+\mathrm{sin}\:{x}}\:= \\ $$$${A}=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{tan}\:{x}}=\mathrm{1} \\ $$$${B}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sec}\:^{\mathrm{2}} {x}−\mathrm{cos}\:{x}\left(\mathrm{1}+\mathrm{tan}\:{x}\right)}{{x}\mathrm{cos}\:{x}+\mathrm{sin}\:{x}} \\ $$$${B}=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sec}\:^{\mathrm{2}} {x}−\mathrm{cos}\:{x}−\mathrm{sin}\:{x}}{{x}\mathrm{cos}\:{x}+\mathrm{sin}\:{x}} \\ $$$${B}=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{\:\:\mathrm{cos}\:^{\mathrm{2}} {x}}×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\mathrm{cos}\:^{\mathrm{3}} {x}−\left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} {x}\right)\mathrm{sin}\:{x}}{{x}\mathrm{cos}\:{x}+\mathrm{sin}\:{x}} \\ $$$${B}=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{3cos}\:^{\mathrm{2}} {x}\mathrm{sin}\:{x}−\mathrm{cos}\:{x}+\mathrm{3sin}\:^{\mathrm{2}} {x}\mathrm{cos}\:{x}}{−{x}\mathrm{sin}\:{x}+\mathrm{cos}\:{x}+\mathrm{cos}\:{x}} \\ $$$${B}=−\frac{\mathrm{1}}{\mathrm{2}}\:\Leftrightarrow\:{A}×{B}\:=\:−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$
Commented by jagoll last updated on 02/Feb/20
$${thank}\:{you}\:{mister} \\ $$
