Question Number 146119 by liberty last updated on 11/Jul/21
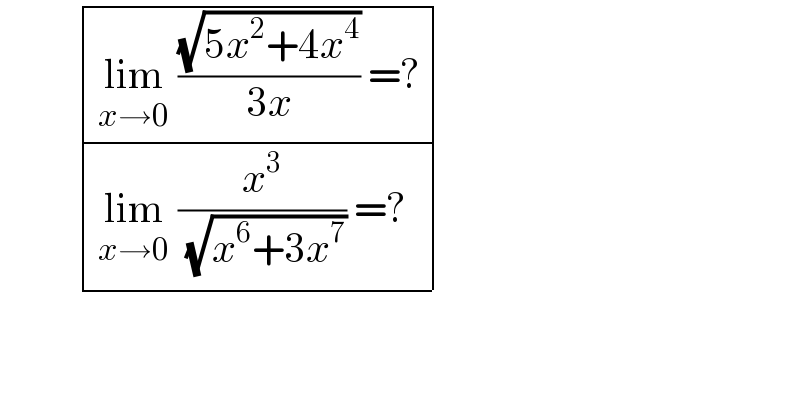
$$\:\:\:\:\:\:\:\:\:\begin{array}{|c|c|}{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{5}{x}^{\mathrm{2}} +\mathrm{4}{x}^{\mathrm{4}} }}{\mathrm{3}{x}}\:=?}\\{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{3}} }{\:\sqrt{{x}^{\mathrm{6}} +\mathrm{3}{x}^{\mathrm{7}} }}\:=?}\\\hline\end{array} \\ $$
Commented by ajfour last updated on 11/Jul/21

$${you}\:{have}\:{been}\:{on}\:{this}\:{forum}, \\ $$$${quite}\:{a}\:{while},\:{haven}'{t}\:{you} \\ $$$${grasped}\:{this}\:{much}-\:{i}\:{mean} \\ $$$${order}\:{of}\:{infinitesimals}.. \\ $$
Commented by EDWIN88 last updated on 11/Jul/21

$$ \\ $$.does everyone who posts on this forum say he doesn't understand? you are very wrong. many who post just so there is material for discussion.
Answered by gsk2684 last updated on 11/Jul/21

$$\underset{{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}\frac{\mid{x}\mid\sqrt{\mathrm{5}+\mathrm{4}{x}^{\mathrm{2}} }}{\mathrm{3}{x}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−{x}\sqrt{\mathrm{5}+\mathrm{4}{x}^{\mathrm{2}} }}{\mathrm{3}{x}}=\frac{−\sqrt{\mathrm{5}}}{\mathrm{3}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{\mid{x}\mid\sqrt{\mathrm{5}+\mathrm{4}{x}^{\mathrm{2}} }}{\mathrm{3}{x}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}\sqrt{\mathrm{5}+\mathrm{4}{x}^{\mathrm{2}} }}{\mathrm{3}{x}}=\frac{\sqrt{\mathrm{5}}}{\mathrm{3}} \\ $$$${limit}\:{does}\:{not}\:{exist}\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}\frac{{x}^{\mathrm{3}} }{\mid{x}^{\mathrm{3}} \mid\sqrt{\mathrm{1}+\mathrm{3}{x}}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}^{\mathrm{3}} }{−{x}^{\mathrm{3}} \sqrt{\mathrm{1}+\mathrm{3}{x}}}=−\mathrm{1}\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{{x}^{\mathrm{3}} }{\mid{x}^{\mathrm{3}} \mid\sqrt{\mathrm{1}+\mathrm{3}{x}}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}^{\mathrm{3}} }{{x}^{\mathrm{3}} \sqrt{\mathrm{1}+\mathrm{3}{x}}}=\mathrm{1} \\ $$$${limit}\:{does}\:{not}\:{exist}\:\: \\ $$
Answered by ajfour last updated on 11/Jul/21

$$\left({i}\right)\:\:\:{L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\sqrt{\mathrm{5}+\mathrm{4}{x}^{\mathrm{2}} }}{\mathrm{3}{s}}=\frac{\sqrt{\mathrm{5}}}{\mathrm{3}}{s} \\ $$$$\:\:\:\:\:\:\:\:{s}=\mathrm{1}\:\:{if}\:{x}>\mathrm{0}\:, \\ $$$$\:\:\:\:\:\:\:\:{s}=−\mathrm{1}\:\:{if}\:{x}<\mathrm{0} \\ $$$${so}\:{limit}\:{dont}\:{exist}\:{at}\:{x}=\mathrm{0}. \\ $$$$\left({ii}\right)\:{L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{s}}{\:\sqrt{\mathrm{1}+\mathrm{3}{x}}}={s} \\ $$$$\:\Rightarrow\:{limit}\:{dont}\:{exist}. \\ $$
Answered by hknkrc46 last updated on 11/Jul/21

$$\left(\mathrm{1}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{5}\boldsymbol{{x}}^{\mathrm{2}} \:+\:\mathrm{4}\boldsymbol{{x}}^{\mathrm{4}} }}{\mathrm{3}\boldsymbol{{x}}}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\boldsymbol{{x}}^{\mathrm{2}} \left(\mathrm{5}\:+\:\mathrm{4}\boldsymbol{{x}}^{\mathrm{2}} \right)}}{\mathrm{3}\boldsymbol{{x}}} \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\boldsymbol{{x}}\sqrt{\mathrm{5}\:+\:\mathrm{4}\boldsymbol{{x}}^{\mathrm{2}} }}{\mathrm{3}\boldsymbol{{x}}}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{5}\:+\:\mathrm{4}\boldsymbol{{x}}^{\mathrm{2}} }}{\mathrm{3}}\:=\:\frac{\sqrt{\mathrm{5}}}{\mathrm{3}} \\ $$$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\boldsymbol{{x}}^{\mathrm{3}} }{\:\sqrt{\boldsymbol{{x}}^{\mathrm{6}} \:+\:\mathrm{3}\boldsymbol{{x}}^{\mathrm{7}} }}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\boldsymbol{{x}}^{\mathrm{3}} }{\:\sqrt{\boldsymbol{{x}}^{\mathrm{6}} \left(\mathrm{1}\:+\:\mathrm{3}\boldsymbol{{x}}\right)}} \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\boldsymbol{{x}}^{\mathrm{3}} }{\boldsymbol{{x}}^{\mathrm{3}} \sqrt{\mathrm{1}\:+\:\mathrm{3}\boldsymbol{{x}}}}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}\:+\:\mathrm{3}\boldsymbol{{x}}}}\:=\:\mathrm{1} \\ $$
Commented by lyubita last updated on 11/Jul/21

$${wrong}\:{answers} \\ $$
Commented by henderson last updated on 14/Jul/21

$$\mathrm{0}\:\notin\:\boldsymbol{\mathrm{Domain}}\:\boldsymbol{\mathrm{of}}\:\:\boldsymbol{\mathrm{expressions}}\:. \\ $$$$\boldsymbol{\mathrm{so}}\:\boldsymbol{\mathrm{you}}\:\boldsymbol{\mathrm{need}}\:\boldsymbol{\mathrm{to}}\:\boldsymbol{\mathrm{compare}}\:\underset{{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}\:\:\:\:\:\boldsymbol{\mathrm{and}}\:\:\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\:\:. \\ $$
