Question Number 66795 by mathmax by abdo last updated on 19/Aug/19
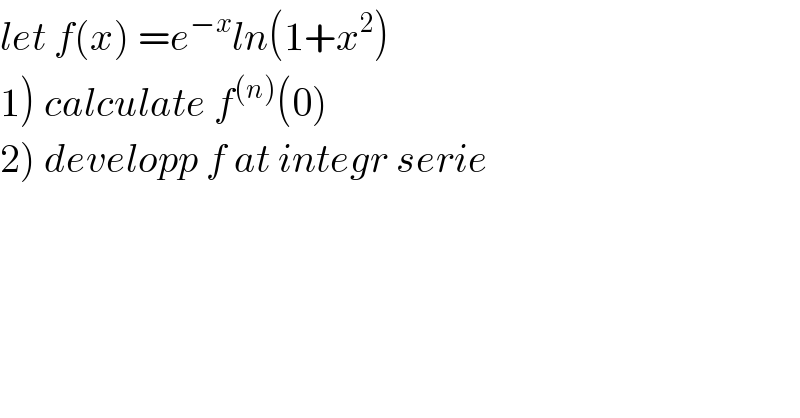
$${let}\:{f}\left({x}\right)\:={e}^{−{x}} {ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right) \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{f}^{\left({n}\right)} \left(\mathrm{0}\right) \\ $$$$\left.\mathrm{2}\right)\:{developp}\:{f}\:{at}\:{integr}\:{serie} \\ $$
Commented by mathmax by abdo last updated on 26/Aug/19

$$\left.\mathrm{1}\right)\:{we}\:{have}\:{f}\left({x}\right)\:={e}^{−{x}} {ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\:\Rightarrow \\ $$$${f}^{\left({n}\right)} \left({x}\right)\:=\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \left({ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\right)^{\left({k}\right)} \:\left({e}^{−{x}} \right)^{\left({n}−{k}\right)} \\ $$$$=\left(−\mathrm{1}\right)^{{n}} \:{e}^{−{x}} {ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\:+\sum_{{k}=\mathrm{1}} ^{{n}} \:{C}_{{n}} ^{{k}} \left\{{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\right\}^{\left({k}\right)} \left({e}^{−{x}} \right)^{\left({n}−{k}\right)} \\ $$$$\left({ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\right)^{\left(\mathrm{1}\right)} \:=\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }\:\Rightarrow\left\{{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\right\}^{\left({k}\right)} \:=\left(\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }\right)^{\left({k}−\mathrm{1}\right)} \\ $$$$=\left(\frac{\mathrm{2}{x}}{\left({x}−{i}\right)\left({x}+{i}\right)}\right)^{\left({k}−\mathrm{1}\right)} =\left\{\frac{\mathrm{1}}{{x}+{i}}+\frac{\mathrm{1}}{{x}−{i}}\right\}^{\left({k}−\mathrm{1}\right)} =\frac{\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} \left({k}−\mathrm{1}\right)!}{\left({x}+{i}\right)^{{k}} } \\ $$$$+\frac{\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} \left({k}−\mathrm{1}\right)!}{\left({x}−{i}\right)^{{k}} }\:=\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} \left({k}−\mathrm{1}\right)!\left\{\frac{\mathrm{1}}{\left({x}+{i}\right)^{{k}} }+\frac{\mathrm{1}}{\left({x}−{i}\right)^{{k}} }\right\} \\ $$$$=\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} \left({k}−\mathrm{1}\right)!×\frac{\mathrm{2}{Re}\left(\left({x}+{i}\right)^{{k}} \right)}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{{k}} }\:\Rightarrow \\ $$$${f}^{\left({n}\right)} \left({x}\right)\:=\left(−\mathrm{1}\right)^{{n}} \:{e}^{−{x}} {ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right) \\ $$$$+\sum_{{k}=\mathrm{1}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\:\:\frac{\mathrm{2}\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} \left({k}−\mathrm{1}\right)!\:{Re}\left(\left({x}+{i}\right)^{{k}} \right)}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{{k}} }×\left(−\mathrm{1}\right)^{{n}−{k}} \:{e}^{−{x}} \\ $$$$\Rightarrow{f}^{\left({n}\right)} \left(\mathrm{0}\right)\:=\sum_{{k}=\mathrm{1}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\mathrm{2}\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} \left({k}−\mathrm{1}\right)!{cos}\left(\frac{{k}\pi}{\mathrm{2}}\right)\left(−\mathrm{1}\right)^{{n}−{k}} \\ $$$$=\mathrm{2}\sum_{{k}=\mathrm{1}} ^{{n}} \:\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \:{C}_{{n}} ^{{k}} \:\:{cos}\left(\frac{{k}\pi}{\mathrm{2}}\right) \\ $$$$ \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 26/Aug/19
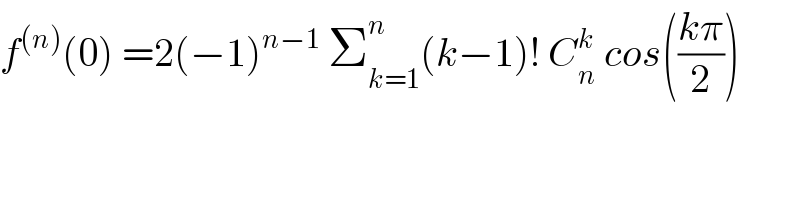
$${f}^{\left({n}\right)} \left(\mathrm{0}\right)\:=\mathrm{2}\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \:\sum_{{k}=\mathrm{1}} ^{{n}} \left({k}−\mathrm{1}\right)!\:{C}_{{n}} ^{{k}} \:{cos}\left(\frac{{k}\pi}{\mathrm{2}}\right) \\ $$
Commented by mathmax by abdo last updated on 26/Aug/19
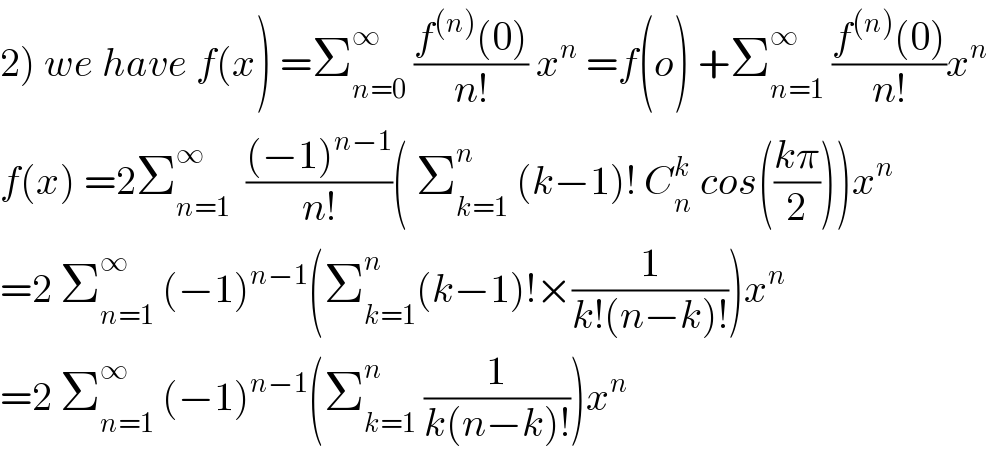
$$\left.\mathrm{2}\right)\:{we}\:{have}\:{f}\left({x}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{f}^{\left({n}\right)} \left(\mathrm{0}\right)}{{n}!}\:{x}^{{n}} \:={f}\left({o}\right)\:+\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{f}^{\left({n}\right)} \left(\mathrm{0}\right)}{{n}!}{x}^{{n}} \\ $$$${f}\left({x}\right)\:=\mathrm{2}\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}!}\left(\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\left({k}−\mathrm{1}\right)!\:{C}_{{n}} ^{{k}} \:{cos}\left(\frac{{k}\pi}{\mathrm{2}}\right)\right){x}^{{n}} \\ $$$$=\mathrm{2}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left(\sum_{{k}=\mathrm{1}} ^{{n}} \left({k}−\mathrm{1}\right)!×\frac{\mathrm{1}}{{k}!\left({n}−{k}\right)!}\right){x}^{{n}} \\ $$$$=\mathrm{2}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left(\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}\left({n}−{k}\right)!}\right){x}^{{n}} \\ $$
