Menu Close

lim-x-2-x-2-4-tan-pi-x-

Tinku Tara 0 Comments
Pin




Question Number 146170 by EDWIN88 last updated on 11/Jul/21
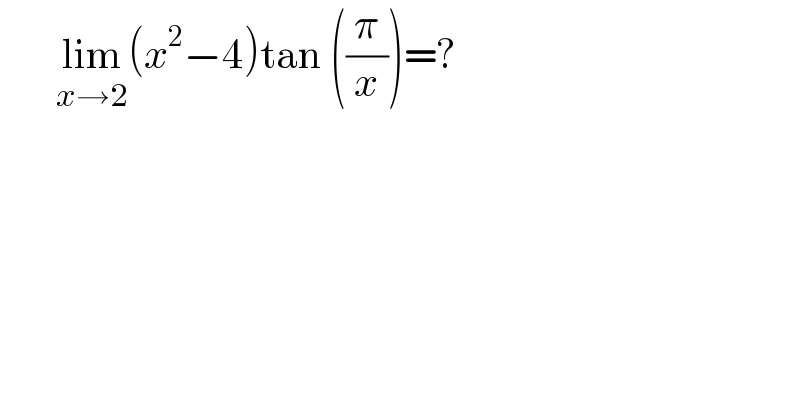
lim_(x→2) (x^2 −4)tan ((π/x))=?
$$\:\:\:\:\:\:\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\left({x}^{\mathrm{2}} −\mathrm{4}\right)\mathrm{tan}\:\left(\frac{\pi}{{x}}\right)=? \\ $$
Answered by iloveisrael last updated on 11/Jul/21
Answered by mathmax by abdo last updated on 11/Jul/21
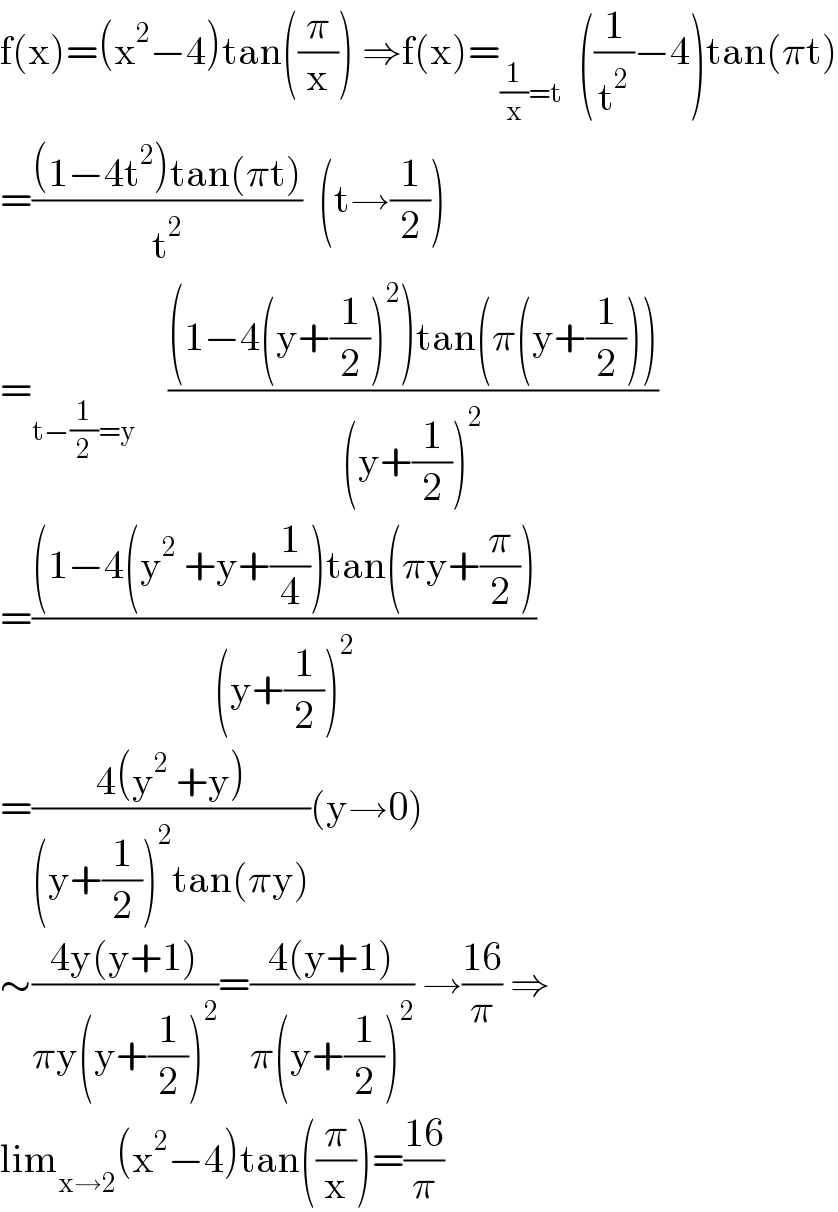
f(x)=(x^2 −4)tan((π/x)) ⇒f(x)=_((1/x)=t) ((1/t^2 )−4)tan(πt) =(((1−4t^2 )tan(πt))/t^2 ) (t→(1/2)) =_(t−(1/2)=y) (((1−4(y+(1/2))^2 )tan(π(y+(1/2))))/((y+(1/2))^2 )) =(((1−4(y^2 +y+(1/4))tan(πy+(π/2)))/((y+(1/2))^2 )) =((4(y^2 +y))/((y+(1/2))^2 tan(πy)))(y→0) ∼((4y(y+1))/(πy(y+(1/2))^2 ))=((4(y+1))/(π(y+(1/2))^2 )) →((16)/π) ⇒ lim_(x→2) (x^2 −4)tan((π/x))=((16)/π)
$$\mathrm{f}\left(\mathrm{x}\right)=\left(\mathrm{x}^{\mathrm{2}} −\mathrm{4}\right)\mathrm{tan}\left(\frac{\pi}{\mathrm{x}}\right)\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=_{\frac{\mathrm{1}}{\mathrm{x}}=\mathrm{t}} \:\:\left(\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }−\mathrm{4}\right)\mathrm{tan}\left(\pi\mathrm{t}\right) \\ $$$$=\frac{\left(\mathrm{1}−\mathrm{4t}^{\mathrm{2}} \right)\mathrm{tan}\left(\pi\mathrm{t}\right)}{\mathrm{t}^{\mathrm{2}} }\:\:\left(\mathrm{t}\rightarrow\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$=_{\mathrm{t}−\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{y}} \:\:\:\:\frac{\left(\mathrm{1}−\mathrm{4}\left(\mathrm{y}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \right)\mathrm{tan}\left(\pi\left(\mathrm{y}+\frac{\mathrm{1}}{\mathrm{2}}\right)\right)}{\left(\mathrm{y}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$=\frac{\left(\mathrm{1}−\mathrm{4}\left(\mathrm{y}^{\mathrm{2}} \:+\mathrm{y}+\frac{\mathrm{1}}{\mathrm{4}}\right)\mathrm{tan}\left(\pi\mathrm{y}+\frac{\pi}{\mathrm{2}}\right)\right.}{\left(\mathrm{y}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{4}\left(\mathrm{y}^{\mathrm{2}} \:+\mathrm{y}\right)}{\left(\mathrm{y}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \mathrm{tan}\left(\pi\mathrm{y}\right)}\left(\mathrm{y}\rightarrow\mathrm{0}\right) \\ $$$$\sim\frac{\mathrm{4y}\left(\mathrm{y}+\mathrm{1}\right)}{\pi\mathrm{y}\left(\mathrm{y}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }=\frac{\mathrm{4}\left(\mathrm{y}+\mathrm{1}\right)}{\pi\left(\mathrm{y}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }\:\rightarrow\frac{\mathrm{16}}{\pi}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} −\mathrm{4}\right)\mathrm{tan}\left(\frac{\pi}{\mathrm{x}}\right)=\frac{\mathrm{16}}{\pi} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *