Question Number 66796 by mathmax by abdo last updated on 19/Aug/19
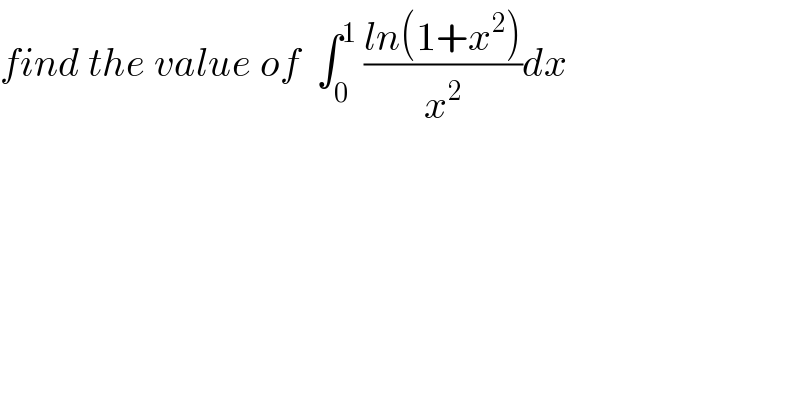
$${find}\:{the}\:{value}\:{of}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} }{dx} \\ $$
Commented by mathmax by abdo last updated on 20/Aug/19
![let I =∫_0 ^1 ((ln(1+x^2 ))/x^2 )dx by parts u^′ =(1/x^2 ) and v=ln(1+x^2 ) ⇒ I =[−(1/x)ln(1+x^2 )]_0 ^1 −∫_0 ^1 (−(1/x))((2x)/(1+x^2 ))dx =−ln(2) +∫_0 ^1 (2/(1+x^2 ))dx =−ln(2)+2[arctanx]_0 ^1 =−ln(2)+2((π/4)) =(π/2)−ln(2) rest to prove that lim_(x→0) ((ln(1+x^2 ))/x) =0 =lim_(x→0) x ((ln(1+x^2 ))/x^2 ) =0 because lim_(u→0) ((ln(1+u))/u) =1](https://www.tinkutara.com/question/Q66935.png)
$${let}\:{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} }{dx}\:\:{by}\:{parts}\:\:{u}^{'} =\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:{and}\:{v}={ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\:\Rightarrow \\ $$$${I}\:=\left[−\frac{\mathrm{1}}{{x}}{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \left(−\frac{\mathrm{1}}{{x}}\right)\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$=−{ln}\left(\mathrm{2}\right)\:+\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{2}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:=−{ln}\left(\mathrm{2}\right)+\mathrm{2}\left[{arctanx}\right]_{\mathrm{0}} ^{\mathrm{1}} \:=−{ln}\left(\mathrm{2}\right)+\mathrm{2}\left(\frac{\pi}{\mathrm{4}}\right) \\ $$$$=\frac{\pi}{\mathrm{2}}−{ln}\left(\mathrm{2}\right)\:{rest}\:{to}\:{prove}\:{that}\:{lim}_{{x}\rightarrow\mathrm{0}} \:\:\frac{{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{{x}}\:=\mathrm{0} \\ $$$$={lim}_{{x}\rightarrow\mathrm{0}} \:\:{x}\:\frac{{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} }\:=\mathrm{0}\:\:{because}\:{lim}_{{u}\rightarrow\mathrm{0}} \:\:\frac{{ln}\left(\mathrm{1}+{u}\right)}{{u}}\:=\mathrm{1} \\ $$
Commented by mathmax by abdo last updated on 20/Aug/19
![remark we have ln^′ (1+u) =(1/(1+u)) =Σ_(n=0) ^∞ (−1)^n u^n if ∣u∣<1 ⇒ ln(1+u) =Σ_(n=0) ^∞ (((−1)^n )/(n+1))u^(n+1) =Σ_(n=1) ^∞ (((−1)^(n−1) u^n )/n) =−Σ_(n=1) ^∞ (((−1)^n )/n)u^n ⇒ln(1+x^2 ) =−Σ_(n=1) ^∞ (((−1)^n )/n) x^(2n) ⇒((ln(1+x^2 ))/x^2 ) =−Σ_(n=1) ^∞ (((−1)^n )/n)x^(2n−2) ⇒∫_0 ^1 ((ln(1+x^2 ))/x^2 )dx =−Σ_(n=1) ^∞ (((−1)^n )/n) [(1/(2n−1))x^(2n−1) ]_0 ^1 =−Σ_(n=1) ^∞ (((−1)^n )/(n(2n−1))) =(π/2)−ln(2) ⇒Σ_(n=1) ^∞ (((−1)^n )/(n(2n−1))) =ln(2)−(π/2)](https://www.tinkutara.com/question/Q66936.png)
$${remark}\:\:{we}\:{have}\:{ln}^{'} \left(\mathrm{1}+{u}\right)\:=\frac{\mathrm{1}}{\mathrm{1}+{u}}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} {u}^{{n}} \:{if}\:\mid{u}\mid<\mathrm{1}\:\Rightarrow \\ $$$${ln}\left(\mathrm{1}+{u}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{1}}{u}^{{n}+\mathrm{1}} \:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} {u}^{{n}} }{{n}}\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}{u}^{{n}} \\ $$$$\Rightarrow{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}\:{x}^{\mathrm{2}{n}} \:\Rightarrow\frac{{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} }\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}{x}^{\mathrm{2}{n}−\mathrm{2}} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} }{dx}\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}\:\left[\frac{\mathrm{1}}{\mathrm{2}{n}−\mathrm{1}}{x}^{\mathrm{2}{n}−\mathrm{1}} \right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}\left(\mathrm{2}{n}−\mathrm{1}\right)}\:=\frac{\pi}{\mathrm{2}}−{ln}\left(\mathrm{2}\right)\:\Rightarrow\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}\left(\mathrm{2}{n}−\mathrm{1}\right)}\:={ln}\left(\mathrm{2}\right)−\frac{\pi}{\mathrm{2}} \\ $$
