Question Number 15263 by Tinkutara last updated on 08/Jun/17
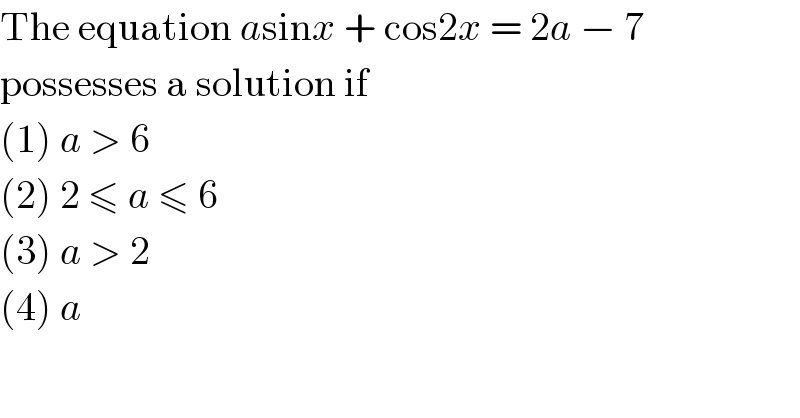
$$\mathrm{The}\:\mathrm{equation}\:{a}\mathrm{sin}{x}\:+\:\mathrm{cos2}{x}\:=\:\mathrm{2}{a}\:−\:\mathrm{7} \\ $$$$\mathrm{possesses}\:\mathrm{a}\:\mathrm{solution}\:\mathrm{if} \\ $$$$\left(\mathrm{1}\right)\:{a}\:>\:\mathrm{6} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{2}\:\leqslant\:{a}\:\leqslant\:\mathrm{6} \\ $$$$\left(\mathrm{3}\right)\:{a}\:>\:\mathrm{2} \\ $$$$\left(\mathrm{4}\right)\:{a} \\ $$
Answered by ajfour last updated on 08/Jun/17

$${a}\mathrm{sin}\:{x}+\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} {x}=\mathrm{2}{a}−\mathrm{7} \\ $$$$\mathrm{sin}\:^{\mathrm{2}} {x}−\frac{{a}}{\mathrm{2}}\mathrm{sin}\:{x}=\mathrm{4}−{a} \\ $$$$\left(\mathrm{sin}\:{x}−\frac{{a}}{\mathrm{4}}\right)^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} }{\mathrm{16}}−{a}+\mathrm{4} \\ $$$$\left(\mathrm{sin}\:{x}−\frac{{a}}{\mathrm{4}}\right)^{\mathrm{2}} =\left(\frac{{a}}{\mathrm{4}}−\mathrm{2}\right)^{\mathrm{2}} \\ $$$$\mid\mathrm{sin}\:{x}−\frac{{a}}{\mathrm{4}}\mid=\mid\frac{{a}}{\mathrm{4}}−\mathrm{2}\mid \\ $$$$\Rightarrow\:\frac{{a}}{\mathrm{4}}−\mathrm{2}=\pm\mid\mathrm{sin}\:{x}−\frac{{a}}{\mathrm{4}}\mid \\ $$$${with}\:{the}\:−{ve}\:{sign},\:{above}\:{eqn}.\:\Rightarrow \\ $$$${no}\:{value}\:{of}\:\boldsymbol{{a}}\:{to}\:{fulfill}\:{the}\:{condition}; \\ $$$${with}\:{the}\:+{ve}\:{sign}\:{it}\:{implies} \\ $$$$\frac{{a}}{\mathrm{2}}=\mathrm{2}+\mathrm{sin}\:{x} \\ $$$${or}\:\:{a}=\mathrm{4}+\mathrm{2sin}\:{x} \\ $$$${As}\:\:−\mathrm{1}\leqslant\mathrm{sin}\:{x}\leqslant\mathrm{1} \\ $$$${we}\:{can}\:{conclude}\:{that} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{2}\leqslant\:\boldsymbol{{a}}\:\leqslant\:\mathrm{6}\:\:\:. \\ $$
Commented by Tinkutara last updated on 09/Jun/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
