Question Number 80823 by M±th+et£s last updated on 06/Feb/20
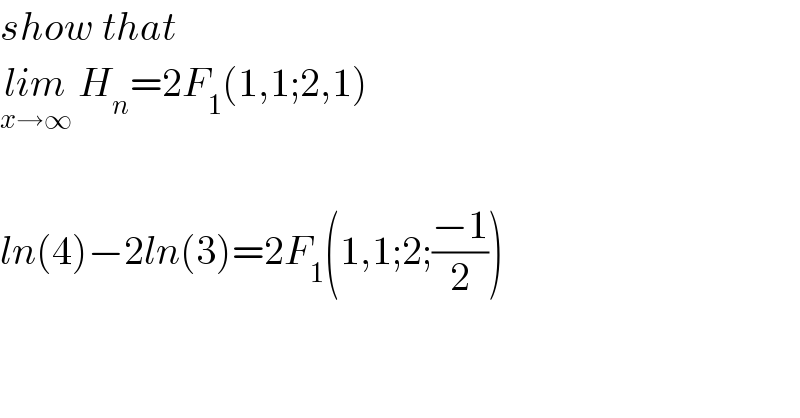
$${show}\:{that}\: \\ $$$$\underset{{x}\rightarrow\infty} {{lim}}\:{H}_{{n}} =\mathrm{2}{F}_{\mathrm{1}} \left(\mathrm{1},\mathrm{1};\mathrm{2},\mathrm{1}\right) \\ $$$$ \\ $$$${ln}\left(\mathrm{4}\right)−\mathrm{2}{ln}\left(\mathrm{3}\right)=\mathrm{2}{F}_{\mathrm{1}} \left(\mathrm{1},\mathrm{1};\mathrm{2};\frac{−\mathrm{1}}{\mathrm{2}}\right) \\ $$
Answered by ~blr237~ last updated on 07/Feb/20
![knowing that _2 F_1 (a,b,c,z)=(1/(B(b,c−b)))∫_0 ^1 x^(b−1) (1−x)^(c−b−1) (1−zx)^(−a) dx _2 F_1 (1,1,2,1)=(1/(B(1,2−1)))∫_0 ^1 x^(1−1) (1−x)^(2−1−1) (1− 1×x)^(−1) dx = ((Γ(2))/(Γ(1)Γ(1))) ∫_0 ^1 (1/(1−x))dx =Σ_(n=0) ^∞ ∫_0 ^1 x^n dx =Σ_(n=0) ^∞ (1/(n+1)) =lim_(n→∞) Σ_(p=1) ^(n+1) (1/p) _2 F_1 (1,1,2,−(1/2))= (1/(B(1,1)))∫_0 ^1 (1/(1+(x/2)))dx=[2ln(1+(x/2))]_0 ^1 =2ln((3/2))=2ln3−ln4](https://www.tinkutara.com/question/Q80854.png)
$${knowing}\:{that}\:\:_{\mathrm{2}} {F}_{\mathrm{1}} \left({a},{b},{c},{z}\right)=\frac{\mathrm{1}}{{B}\left({b},{c}−{b}\right)}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{b}−\mathrm{1}} \left(\mathrm{1}−{x}\right)^{{c}−{b}−\mathrm{1}} \left(\mathrm{1}−{zx}\right)^{−{a}} {dx} \\ $$$$\:_{\mathrm{2}} {F}_{\mathrm{1}} \left(\mathrm{1},\mathrm{1},\mathrm{2},\mathrm{1}\right)=\frac{\mathrm{1}}{{B}\left(\mathrm{1},\mathrm{2}−\mathrm{1}\right)}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{1}−\mathrm{1}} \left(\mathrm{1}−{x}\right)^{\mathrm{2}−\mathrm{1}−\mathrm{1}} \left(\mathrm{1}−\:\mathrm{1}×{x}\right)^{−\mathrm{1}} {dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\Gamma\left(\mathrm{2}\right)}{\Gamma\left(\mathrm{1}\right)\Gamma\left(\mathrm{1}\right)}\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}−{x}}{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} {dx}\:=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{{n}+\mathrm{1}}\:=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\underset{{p}=\mathrm{1}} {\overset{{n}+\mathrm{1}} {\sum}}\frac{\mathrm{1}}{{p}}\: \\ $$$$\:\:_{\mathrm{2}} {F}_{\mathrm{1}} \left(\mathrm{1},\mathrm{1},\mathrm{2},−\frac{\mathrm{1}}{\mathrm{2}}\right)=\:\frac{\mathrm{1}}{{B}\left(\mathrm{1},\mathrm{1}\right)}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+\frac{{x}}{\mathrm{2}}}{dx}=\left[\mathrm{2}{ln}\left(\mathrm{1}+\frac{{x}}{\mathrm{2}}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} =\mathrm{2}{ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)=\mathrm{2}{ln}\mathrm{3}−{ln}\mathrm{4} \\ $$
Commented by M±th+et£s last updated on 07/Feb/20
$${thank}\:{you}\:{so}\:{much}\:{sir}\:.\:{great} \\ $$
