Question Number 80921 by jagoll last updated on 08/Feb/20
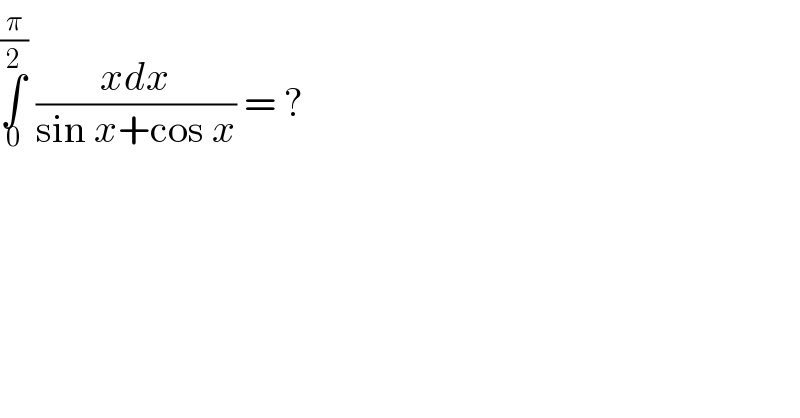
$$\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\frac{{xdx}}{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}\:=\:? \\ $$
Commented by john santu last updated on 08/Feb/20
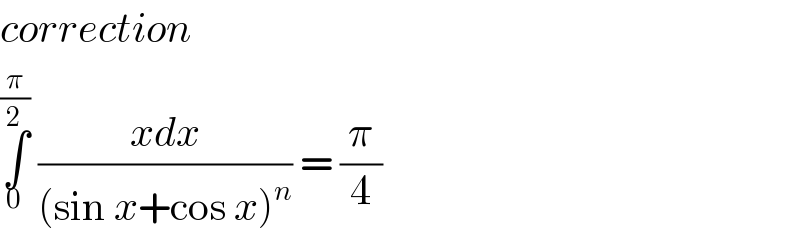
$${correction}\: \\ $$$$\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\frac{{xdx}}{\left(\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\right)^{{n}} }\:=\:\frac{\pi}{\mathrm{4}} \\ $$
Commented by mathmax by abdo last updated on 10/Feb/20
![A=∫_0 ^(π/2) ((xdx)/(sinx +cosx)) changement x=(π/2)−t give A =−∫_0 ^(π/2) ((((π/2)−t)(−dt))/(cost +sint)) =(π/2)∫_0 ^(π/2) (dt/(cost +sint)) −A ⇒ 2A=(π/2) ∫_0 ^(π/2) (dt/(cost +sint)) ⇒A=(π/4) ∫_0 ^(π/2) (dt/(cost +sint)) changement tan((t/2))=u give ∫_0 ^(π/2) (dt/(cost +sint)) =∫_0 ^1 (1/(((1−u^2 )/(1+u^2 ))+((2u)/(1+u^2 ))))×((2du)/(1+u^2 )) =∫_0 ^1 ((2du)/(1−u^2 +2u)) =−2 ∫_0 ^1 (du/(u^2 −2u−1)) =−2 ∫_0 ^1 (du/((u−1)^2 −2)) =−2 ∫_0 ^1 (du/((u−1−(√2))(u−1+(√2)))) =−(2/(2(√2))) ∫_0 ^1 {(1/(u−1−(√2)))−(1/(u−1+(√2)))}du =−(1/( (√2)))[ln∣((u−1−(√2))/(u−1+(√2)))∣]_0 ^1 =−(1/( (√2)))(−ln(((1+(√2))/( (√2)−1))) =(1/( (√2)))ln(((√2)+1)^2 ) =(√2)ln(1+(√2)) ⇒A =((π(√2))/4)ln(1+(√2))](https://www.tinkutara.com/question/Q81176.png)
$${A}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{xdx}}{{sinx}\:+{cosx}}\:\:{changement}\:{x}=\frac{\pi}{\mathrm{2}}−{t}\:{give} \\ $$$${A}\:=−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\left(\frac{\pi}{\mathrm{2}}−{t}\right)\left(−{dt}\right)}{{cost}\:+{sint}}\:=\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{dt}}{{cost}\:+{sint}}\:−{A}\:\Rightarrow \\ $$$$\mathrm{2}{A}=\frac{\pi}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{dt}}{{cost}\:+{sint}}\:\Rightarrow{A}=\frac{\pi}{\mathrm{4}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{dt}}{{cost}\:+{sint}} \\ $$$${changement}\:{tan}\left(\frac{{t}}{\mathrm{2}}\right)={u}\:{give} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{dt}}{{cost}\:+{sint}}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}}{\frac{\mathrm{1}−{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} }+\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }}×\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} }\:=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}{du}}{\mathrm{1}−{u}^{\mathrm{2}} \:+\mathrm{2}{u}} \\ $$$$=−\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{du}}{{u}^{\mathrm{2}} −\mathrm{2}{u}−\mathrm{1}}\:=−\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{du}}{\left({u}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}}\:=−\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{du}}{\left({u}−\mathrm{1}−\sqrt{\mathrm{2}}\right)\left({u}−\mathrm{1}+\sqrt{\mathrm{2}}\right)} \\ $$$$=−\frac{\mathrm{2}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \left\{\frac{\mathrm{1}}{{u}−\mathrm{1}−\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{{u}−\mathrm{1}+\sqrt{\mathrm{2}}}\right\}{du} \\ $$$$=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left[{ln}\mid\frac{{u}−\mathrm{1}−\sqrt{\mathrm{2}}}{{u}−\mathrm{1}+\sqrt{\mathrm{2}}}\mid\right]_{\mathrm{0}} ^{\mathrm{1}} \:=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(−{ln}\left(\frac{\mathrm{1}+\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}\right)\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{ln}\left(\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{2}} \right)\right. \\ $$$$=\sqrt{\mathrm{2}}{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\:\Rightarrow{A}\:=\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{4}}{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right) \\ $$
