Question Number 146602 by mnjuly1970 last updated on 14/Jul/21
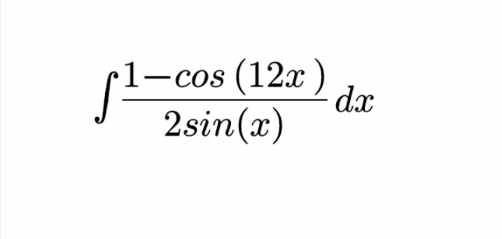
Answered by qaz last updated on 15/Jul/21
![∫((1−cos (12x))/(2sin x))dx=∫((sin^2 (6x))/(sin x))dx =4∫(([sin (3x)cos (3x)]^2 )/(sin x))dx =4∫(([(3sin x−4sin^3 x)(4cos^3 x−3cos x)]^2 )/(sin x))dx =4∫sin xcos^2 x[(3−4sin^2 x)(4cos^2 x−3)]^2 dx =4∫SC^2 [(4C^2 −1)(4C^2 −3)]^2 dx =−4∫(256C^(10) −512C^8 +352C^6 −96C^4 +9C^2 )dC =−4(((256)/(11))C^(11) −((512)/9)C^9 +((352)/7)C^7 −((96)/5)C^5 +3C^3 )+K =−((1024)/(11))cos^(11) x+((2048)/9)cos^9 x−((1408)/7)cos^7 x+((384)/5)cos^5 x−12cos^3 x+K](https://www.tinkutara.com/question/Q146743.png)
$$\int\frac{\mathrm{1}−\mathrm{cos}\:\left(\mathrm{12x}\right)}{\mathrm{2sin}\:\mathrm{x}}\mathrm{dx}=\int\frac{\mathrm{sin}\:^{\mathrm{2}} \left(\mathrm{6x}\right)}{\mathrm{sin}\:\mathrm{x}}\mathrm{dx} \\ $$$$=\mathrm{4}\int\frac{\left[\mathrm{sin}\:\left(\mathrm{3x}\right)\mathrm{cos}\:\left(\mathrm{3x}\right)\right]^{\mathrm{2}} }{\mathrm{sin}\:\mathrm{x}}\mathrm{dx} \\ $$$$=\mathrm{4}\int\frac{\left[\left(\mathrm{3sin}\:\mathrm{x}−\mathrm{4sin}\:^{\mathrm{3}} \mathrm{x}\right)\left(\mathrm{4cos}\:^{\mathrm{3}} \mathrm{x}−\mathrm{3cos}\:\mathrm{x}\right)\right]^{\mathrm{2}} }{\mathrm{sin}\:\mathrm{x}}\mathrm{dx} \\ $$$$=\mathrm{4}\int\mathrm{sin}\:\mathrm{xcos}\:^{\mathrm{2}} \mathrm{x}\left[\left(\mathrm{3}−\mathrm{4sin}\:^{\mathrm{2}} \mathrm{x}\right)\left(\mathrm{4cos}\:^{\mathrm{2}} \mathrm{x}−\mathrm{3}\right)\right]^{\mathrm{2}} \mathrm{dx} \\ $$$$=\mathrm{4}\int\mathrm{SC}^{\mathrm{2}} \left[\left(\mathrm{4C}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{4C}^{\mathrm{2}} −\mathrm{3}\right)\right]^{\mathrm{2}} \mathrm{dx} \\ $$$$=−\mathrm{4}\int\left(\mathrm{256C}^{\mathrm{10}} −\mathrm{512C}^{\mathrm{8}} +\mathrm{352C}^{\mathrm{6}} −\mathrm{96C}^{\mathrm{4}} +\mathrm{9C}^{\mathrm{2}} \right)\mathrm{dC} \\ $$$$=−\mathrm{4}\left(\frac{\mathrm{256}}{\mathrm{11}}\mathrm{C}^{\mathrm{11}} −\frac{\mathrm{512}}{\mathrm{9}}\mathrm{C}^{\mathrm{9}} +\frac{\mathrm{352}}{\mathrm{7}}\mathrm{C}^{\mathrm{7}} −\frac{\mathrm{96}}{\mathrm{5}}\mathrm{C}^{\mathrm{5}} +\mathrm{3C}^{\mathrm{3}} \right)+\mathrm{K} \\ $$$$=−\frac{\mathrm{1024}}{\mathrm{11}}\mathrm{cos}\:^{\mathrm{11}} \mathrm{x}+\frac{\mathrm{2048}}{\mathrm{9}}\mathrm{cos}\:^{\mathrm{9}} \mathrm{x}−\frac{\mathrm{1408}}{\mathrm{7}}\mathrm{cos}\:^{\mathrm{7}} \mathrm{x}+\frac{\mathrm{384}}{\mathrm{5}}\mathrm{cos}\:^{\mathrm{5}} \mathrm{x}−\mathrm{12cos}\:^{\mathrm{3}} \mathrm{x}+\mathrm{K} \\ $$
