Menu Close

From-a-point-A-on-the-circum-ference-of-a-circle-of-radius-r-a-perpendicular-AF-is-dropped-on-a-tangent-to-the-circle-at-P-Find-the-maximum-possible-area-of-APF-

Tinku Tara 0 Comments
Pin




Question Number 15736 by ajfour last updated on 13/Jun/17
From a point A on the circum- ference of a circle of radius r, a perpendicular AF is dropped on a tangent to the circle at P. Find the maximum possible area of ΔAPF .
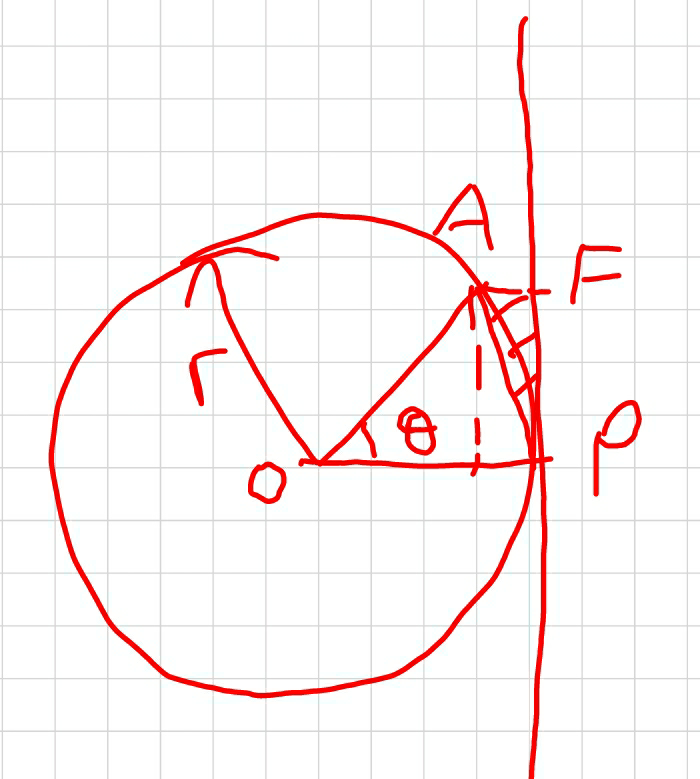
$${From}\:{a}\:{point}\:{A}\:{on}\:{the}\:{circum}- \\ $$$${ference}\:{of}\:{a}\:{circle}\:{of}\:{radius}\:\boldsymbol{{r}},\:{a} \\ $$$${perpendicular}\:{AF}\:\:{is}\:{dropped}\:{on} \\ $$$${a}\:{tangent}\:{to}\:{the}\:{circle}\:{at}\:{P}. \\ $$$${Find}\:{the}\:\:{maximum}\:{possible}\: \\ $$$${area}\:{of}\:\Delta{APF}\:. \\ $$
Answered by mrW1 last updated on 13/Jun/17
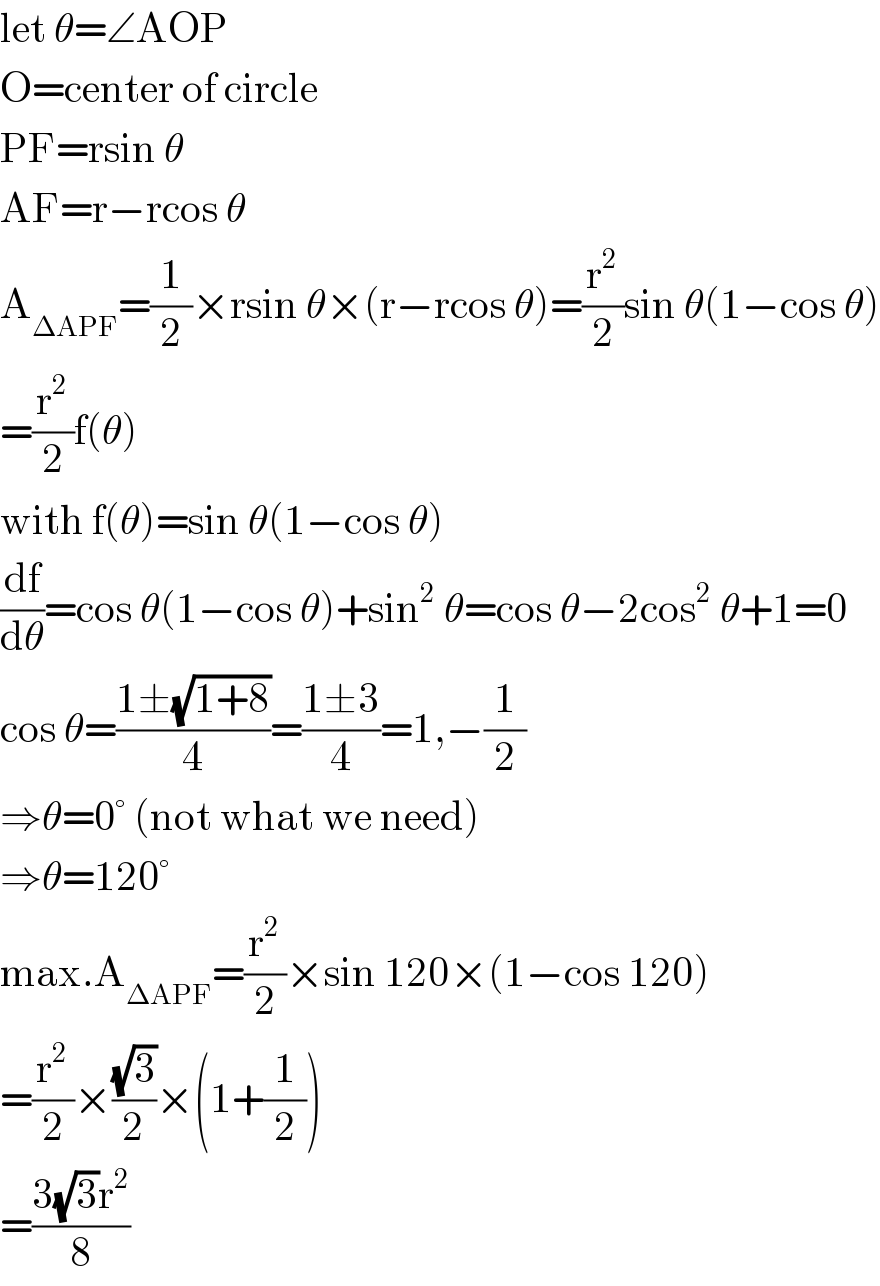
let θ=∠AOP O=center of circle PF=rsin θ AF=r−rcos θ A_(ΔAPF) =(1/2)×rsin θ×(r−rcos θ)=(r^2 /2)sin θ(1−cos θ) =(r^2 /2)f(θ) with f(θ)=sin θ(1−cos θ) (df/dθ)=cos θ(1−cos θ)+sin^2 θ=cos θ−2cos^2 θ+1=0 cos θ=((1±(√(1+8)))/4)=((1±3)/4)=1,−(1/2) ⇒θ=0° (not what we need) ⇒θ=120° max.A_(ΔAPF) =(r^2 /2)×sin 120×(1−cos 120) =(r^2 /2)×((√3)/2)×(1+(1/2)) =((3(√3)r^2 )/8)
$$\mathrm{let}\:\theta=\angle\mathrm{AOP} \\ $$$$\mathrm{O}=\mathrm{center}\:\mathrm{of}\:\mathrm{circle} \\ $$$$\mathrm{PF}=\mathrm{rsin}\:\theta \\ $$$$\mathrm{AF}=\mathrm{r}−\mathrm{rcos}\:\theta \\ $$$$\mathrm{A}_{\Delta\mathrm{APF}} =\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{rsin}\:\theta×\left(\mathrm{r}−\mathrm{rcos}\:\theta\right)=\frac{\mathrm{r}^{\mathrm{2}} }{\mathrm{2}}\mathrm{sin}\:\theta\left(\mathrm{1}−\mathrm{cos}\:\theta\right) \\ $$$$=\frac{\mathrm{r}^{\mathrm{2}} }{\mathrm{2}}\mathrm{f}\left(\theta\right) \\ $$$$\mathrm{with}\:\mathrm{f}\left(\theta\right)=\mathrm{sin}\:\theta\left(\mathrm{1}−\mathrm{cos}\:\theta\right) \\ $$$$\frac{\mathrm{df}}{\mathrm{d}\theta}=\mathrm{cos}\:\theta\left(\mathrm{1}−\mathrm{cos}\:\theta\right)+\mathrm{sin}^{\mathrm{2}} \:\theta=\mathrm{cos}\:\theta−\mathrm{2cos}^{\mathrm{2}} \:\theta+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{cos}\:\theta=\frac{\mathrm{1}\pm\sqrt{\mathrm{1}+\mathrm{8}}}{\mathrm{4}}=\frac{\mathrm{1}\pm\mathrm{3}}{\mathrm{4}}=\mathrm{1},−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\theta=\mathrm{0}°\:\left(\mathrm{not}\:\mathrm{what}\:\mathrm{we}\:\mathrm{need}\right) \\ $$$$\Rightarrow\theta=\mathrm{120}° \\ $$$$\mathrm{max}.\mathrm{A}_{\Delta\mathrm{APF}} =\frac{\mathrm{r}^{\mathrm{2}} }{\mathrm{2}}×\mathrm{sin}\:\mathrm{120}×\left(\mathrm{1}−\mathrm{cos}\:\mathrm{120}\right) \\ $$$$=\frac{\mathrm{r}^{\mathrm{2}} }{\mathrm{2}}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}×\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{3}\sqrt{\mathrm{3}}\mathrm{r}^{\mathrm{2}} }{\mathrm{8}} \\ $$
Commented by mrW1 last updated on 13/Jun/17
Commented by ajfour last updated on 13/Jun/17
great sir, is there also a way of geometry to arrive at the result without having to differentiate..
$${great}\:{sir},\:{is}\:{there}\:{also}\:{a}\:{way} \\ $$$${of}\:{geometry}\:{to}\:{arrive}\:{at}\:{the} \\ $$$${result}\:{without}\:{having}\:{to} \\ $$$${differentiate}.. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *