Quation-posted-Times-ago-i-can-t-find-it-after-Somme-Try-i-got-close-Fofme-0-pi-sin-x-2-dx-pi-3-3-1-F-2-3-4-3-2-7-4-pi-4-4-sin-x-k-0-1-k-x-2k-1-2k-1-sin-x-2-

Question Number 81340 by mind is power last updated on 11/Feb/20

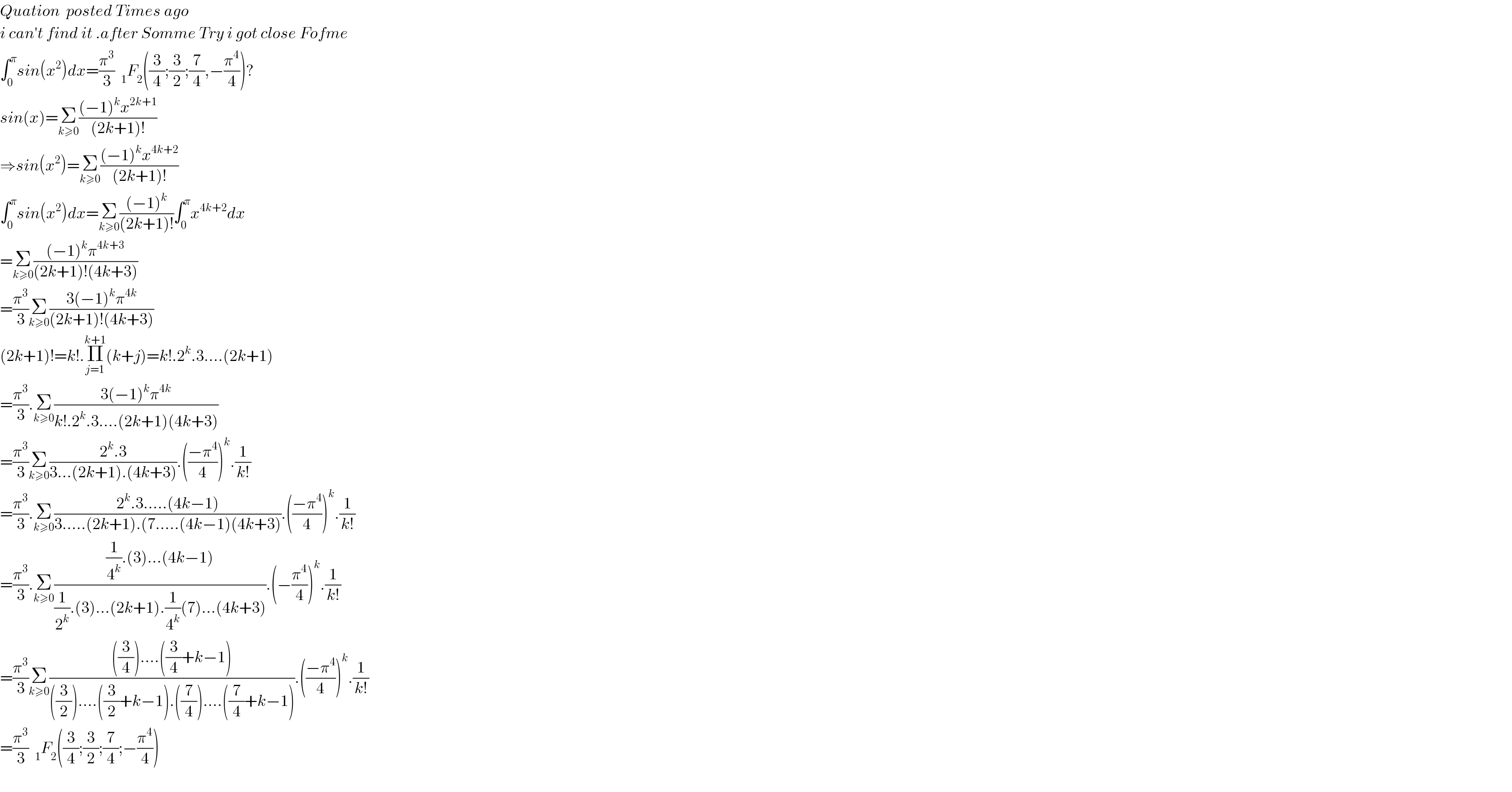
Quation posted Times ago i can′t find it .after Somme Try i got close Fofme ∫_0 ^π sin(x^2 )dx=(π^3 /3) _1 F_2 ((3/4);(3/2);(7/4),−(π^4 /4))? sin(x)=Σ_(k≥0) (((−1)^k x^(2k+1) )/((2k+1)!)) ⇒sin(x^2 )=Σ_(k≥0) (((−1)^k x^(4k+2) )/((2k+1)!)) ∫_0 ^π sin(x^2 )dx=Σ_(k≥0) (((−1)^k )/((2k+1)!))∫_0 ^π x^(4k+2) dx =Σ_(k≥0) (((−1)^k π^(4k+3) )/((2k+1)!(4k+3))) =(π^3 /3)Σ_(k≥0) ((3(−1)^k π^(4k) )/((2k+1)!(4k+3))) (2k+1)!=k!.Π_(j=1) ^(k+1) (k+j)=k!.2^k .3....(2k+1) =(π^3 /3).Σ_(k≥0) ((3(−1)^k π^(4k) )/(k!.2^k .3....(2k+1)(4k+3))) =(π^3 /3)Σ_(k≥0) ((2^k .3)/(3...(2k+1).(4k+3))).(((−π^4 )/4))^k .(1/(k!)) =(π^3 /3).Σ_(k≥0) ((2^k .3.....(4k−1))/(3.....(2k+1).(7.....(4k−1)(4k+3))).(((−π^4 )/4))^k .(1/(k!)) =(π^3 /3).Σ_(k≥0) (((1/4^k ).(3)...(4k−1))/((1/2^k ).(3)...(2k+1).(1/4^k )(7)...(4k+3))).(−(π^4 /4))^k .(1/(k!)) =(π^3 /3)Σ_(k≥0) ((((3/4))....((3/4)+k−1))/(((3/2))....((3/2)+k−1).((7/4))....((7/4)+k−1))).(((−π^4 )/4))^k .(1/(k!)) =(π^3 /3) _1 F_2 ((3/4);(3/2);(7/4);−(π^4 /4))

$${Quation}\:\:{posted}\:{Times}\:{ago} \\ $$$${i}\:{can}'{t}\:{find}\:{it}\:.{after}\:{Somme}\:{Try}\:{i}\:{got}\:{close}\:{Fofme} \\ $$$$\int_{\mathrm{0}} ^{\pi} {sin}\left({x}^{\mathrm{2}} \right){dx}=\frac{\pi^{\mathrm{3}} }{\mathrm{3}}\:\:_{\mathrm{1}} {F}_{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{4}};\frac{\mathrm{3}}{\mathrm{2}};\frac{\mathrm{7}}{\mathrm{4}},−\frac{\pi^{\mathrm{4}} }{\mathrm{4}}\right)? \\ $$$${sin}\left({x}\right)=\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} {x}^{\mathrm{2}{k}+\mathrm{1}} }{\left(\mathrm{2}{k}+\mathrm{1}\right)!} \\ $$$$\Rightarrow{sin}\left({x}^{\mathrm{2}} \right)=\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} {x}^{\mathrm{4}{k}+\mathrm{2}} }{\left(\mathrm{2}{k}+\mathrm{1}\right)!} \\ $$$$\int_{\mathrm{0}} ^{\pi} {sin}\left({x}^{\mathrm{2}} \right){dx}=\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} }{\left(\mathrm{2}{k}+\mathrm{1}\right)!}\int_{\mathrm{0}} ^{\pi} {x}^{\mathrm{4}{k}+\mathrm{2}} {dx} \\ $$$$=\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} \pi^{\mathrm{4}{k}+\mathrm{3}} }{\left(\mathrm{2}{k}+\mathrm{1}\right)!\left(\mathrm{4}{k}+\mathrm{3}\right)} \\ $$$$=\frac{\pi^{\mathrm{3}} }{\mathrm{3}}\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{3}\left(−\mathrm{1}\right)^{{k}} \pi^{\mathrm{4}{k}} }{\left(\mathrm{2}{k}+\mathrm{1}\right)!\left(\mathrm{4}{k}+\mathrm{3}\right)} \\ $$$$\left(\mathrm{2}{k}+\mathrm{1}\right)!={k}!.\underset{{j}=\mathrm{1}} {\overset{{k}+\mathrm{1}} {\prod}}\left({k}+{j}\right)={k}!.\mathrm{2}^{{k}} .\mathrm{3}….\left(\mathrm{2}{k}+\mathrm{1}\right) \\ $$$$=\frac{\pi^{\mathrm{3}} }{\mathrm{3}}.\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{3}\left(−\mathrm{1}\right)^{{k}} \pi^{\mathrm{4}{k}} }{{k}!.\mathrm{2}^{{k}} .\mathrm{3}….\left(\mathrm{2}{k}+\mathrm{1}\right)\left(\mathrm{4}{k}+\mathrm{3}\right)} \\ $$$$=\frac{\pi^{\mathrm{3}} }{\mathrm{3}}\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{2}^{{k}} .\mathrm{3}}{\mathrm{3}…\left(\mathrm{2}{k}+\mathrm{1}\right).\left(\mathrm{4}{k}+\mathrm{3}\right)}.\left(\frac{−\pi^{\mathrm{4}} }{\mathrm{4}}\right)^{{k}} .\frac{\mathrm{1}}{{k}!} \\ $$$$=\frac{\pi^{\mathrm{3}} }{\mathrm{3}}.\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{2}^{{k}} .\mathrm{3}…..\left(\mathrm{4}{k}−\mathrm{1}\right)}{\mathrm{3}…..\left(\mathrm{2}{k}+\mathrm{1}\right).\left(\mathrm{7}…..\left(\mathrm{4}{k}−\mathrm{1}\right)\left(\mathrm{4}{k}+\mathrm{3}\right)\right.}.\left(\frac{−\pi^{\mathrm{4}} }{\mathrm{4}}\right)^{{k}} .\frac{\mathrm{1}}{{k}!} \\ $$$$=\frac{\pi^{\mathrm{3}} }{\mathrm{3}}.\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\frac{\mathrm{1}}{\mathrm{4}^{{k}} }.\left(\mathrm{3}\right)…\left(\mathrm{4}{k}−\mathrm{1}\right)}{\frac{\mathrm{1}}{\mathrm{2}^{{k}} }.\left(\mathrm{3}\right)…\left(\mathrm{2}{k}+\mathrm{1}\right).\frac{\mathrm{1}}{\mathrm{4}^{{k}} }\left(\mathrm{7}\right)…\left(\mathrm{4}{k}+\mathrm{3}\right)}.\left(−\frac{\pi^{\mathrm{4}} }{\mathrm{4}}\right)^{{k}} .\frac{\mathrm{1}}{{k}!} \\ $$$$=\frac{\pi^{\mathrm{3}} }{\mathrm{3}}\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(\frac{\mathrm{3}}{\mathrm{4}}\right)….\left(\frac{\mathrm{3}}{\mathrm{4}}+{k}−\mathrm{1}\right)}{\left(\frac{\mathrm{3}}{\mathrm{2}}\right)….\left(\frac{\mathrm{3}}{\mathrm{2}}+{k}−\mathrm{1}\right).\left(\frac{\mathrm{7}}{\mathrm{4}}\right)….\left(\frac{\mathrm{7}}{\mathrm{4}}+{k}−\mathrm{1}\right)}.\left(\frac{−\pi^{\mathrm{4}} }{\mathrm{4}}\right)^{{k}} .\frac{\mathrm{1}}{{k}!} \\ $$$$=\frac{\pi^{\mathrm{3}} }{\mathrm{3}}\:\:_{\mathrm{1}} {F}_{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{4}};\frac{\mathrm{3}}{\mathrm{2}};\frac{\mathrm{7}}{\mathrm{4}};−\frac{\pi^{\mathrm{4}} }{\mathrm{4}}\right) \\ $$$$ \\ $$

Commented by TawaTawa last updated on 12/Feb/20