Menu Close

given-y-sin-pi-3-2x-2cos-pi-12-x-1-where-x-0-2pi-has-maximum-and-minimum-value-is-p-and-q-find-p-2-q-2-A-18-B-16-C-63-4-D-16-

Tinku Tara 0 Comments
Pin




Question Number 81354 by jagoll last updated on 12/Feb/20
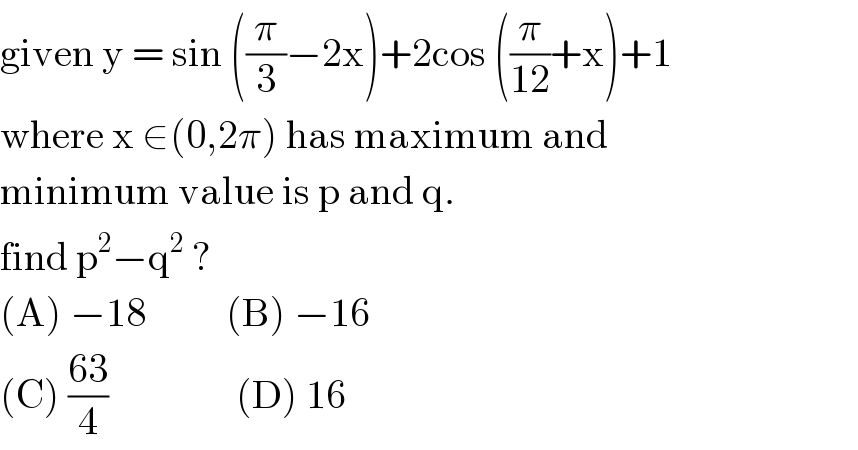
given y = sin ((π/3)−2x)+2cos ((π/(12))+x)+1 where x ∈(0,2π) has maximum and minimum value is p and q. find p^2 −q^2 ? (A) −18 (B) −16 (C) ((63)/4) (D) 16
$$\mathrm{given}\:\mathrm{y}\:=\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−\mathrm{2x}\right)+\mathrm{2cos}\:\left(\frac{\pi}{\mathrm{12}}+\mathrm{x}\right)+\mathrm{1} \\ $$$$\mathrm{where}\:\mathrm{x}\:\in\left(\mathrm{0},\mathrm{2}\pi\right)\:\mathrm{has}\:\mathrm{maximum}\:\mathrm{and} \\ $$$$\mathrm{minimum}\:\mathrm{value}\:\mathrm{is}\:\mathrm{p}\:\mathrm{and}\:\mathrm{q}. \\ $$$$\mathrm{find}\:\mathrm{p}^{\mathrm{2}} −\mathrm{q}^{\mathrm{2}} \:? \\ $$$$\left(\mathrm{A}\right)\:−\mathrm{18}\:\:\:\:\:\:\:\:\:\:\left(\mathrm{B}\right)\:−\mathrm{16} \\ $$$$\left(\mathrm{C}\right)\:\frac{\mathrm{63}}{\mathrm{4}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{D}\right)\:\mathrm{16} \\ $$
Commented by john santu last updated on 12/Feb/20
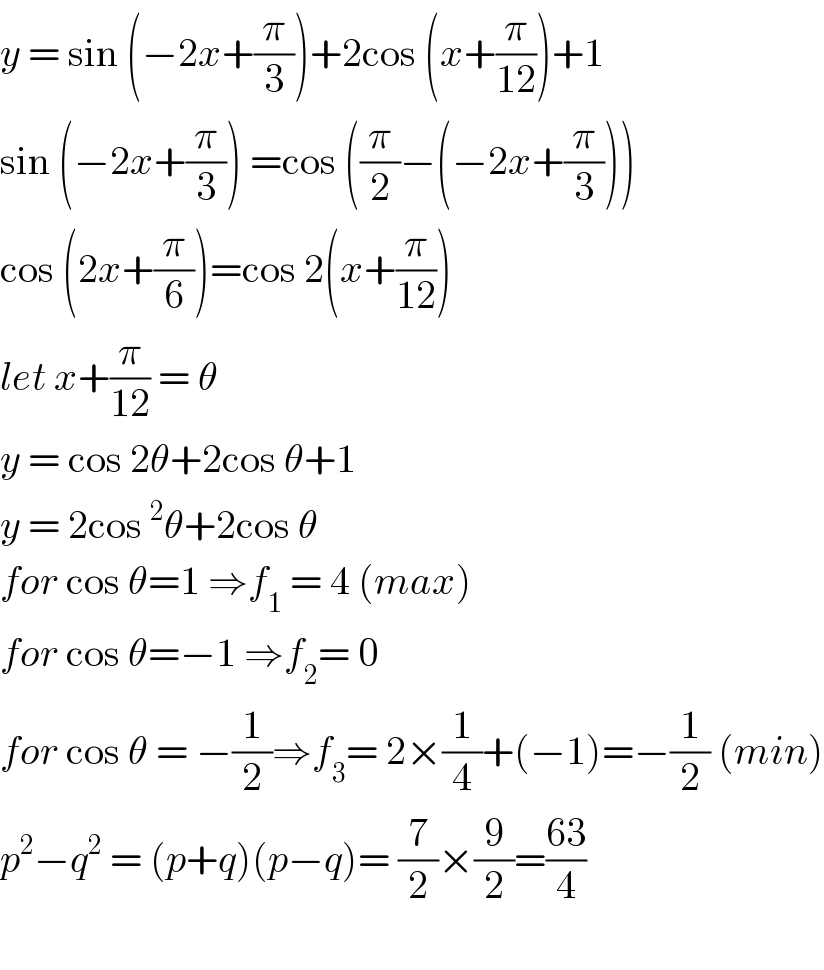
y = sin (−2x+(π/3))+2cos (x+(π/(12)))+1 sin (−2x+(π/3)) =cos ((π/2)−(−2x+(π/3))) cos (2x+(π/6))=cos 2(x+(π/(12))) let x+(π/(12)) = θ y = cos 2θ+2cos θ+1 y = 2cos^2 θ+2cos θ for cos θ=1 ⇒f_1 = 4 (max) for cos θ=−1 ⇒f_2 = 0 for cos θ = −(1/2)⇒f_3 = 2×(1/4)+(−1)=−(1/2) (min) p^2 −q^2 = (p+q)(p−q)= (7/2)×(9/2)=((63)/4)
$${y}\:=\:\mathrm{sin}\:\left(−\mathrm{2}{x}+\frac{\pi}{\mathrm{3}}\right)+\mathrm{2cos}\:\left({x}+\frac{\pi}{\mathrm{12}}\right)+\mathrm{1} \\ $$$$\mathrm{sin}\:\left(−\mathrm{2}{x}+\frac{\pi}{\mathrm{3}}\right)\:=\mathrm{cos}\:\left(\frac{\pi}{\mathrm{2}}−\left(−\mathrm{2}{x}+\frac{\pi}{\mathrm{3}}\right)\right) \\ $$$$\mathrm{cos}\:\left(\mathrm{2}{x}+\frac{\pi}{\mathrm{6}}\right)=\mathrm{cos}\:\mathrm{2}\left({x}+\frac{\pi}{\mathrm{12}}\right) \\ $$$${let}\:{x}+\frac{\pi}{\mathrm{12}}\:=\:\theta \\ $$$${y}\:=\:\mathrm{cos}\:\mathrm{2}\theta+\mathrm{2cos}\:\theta+\mathrm{1} \\ $$$${y}\:=\:\mathrm{2cos}\:^{\mathrm{2}} \theta+\mathrm{2cos}\:\theta \\ $$$${for}\:\mathrm{cos}\:\theta=\mathrm{1}\:\Rightarrow{f}_{\mathrm{1}} \:=\:\mathrm{4}\:\left({max}\right) \\ $$$${for}\:\mathrm{cos}\:\theta=−\mathrm{1}\:\Rightarrow{f}_{\mathrm{2}} =\:\mathrm{0} \\ $$$${for}\:\mathrm{cos}\:\theta\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow{f}_{\mathrm{3}} =\:\mathrm{2}×\frac{\mathrm{1}}{\mathrm{4}}+\left(−\mathrm{1}\right)=−\frac{\mathrm{1}}{\mathrm{2}}\:\left({min}\right) \\ $$$${p}^{\mathrm{2}} −{q}^{\mathrm{2}} \:=\:\left({p}+{q}\right)\left({p}−{q}\right)=\:\frac{\mathrm{7}}{\mathrm{2}}×\frac{\mathrm{9}}{\mathrm{2}}=\frac{\mathrm{63}}{\mathrm{4}} \\ $$$$ \\ $$
Commented by jagoll last updated on 12/Feb/20
thank you
$$\mathrm{thank}\:\mathrm{you} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *