Question Number 146929 by phally last updated on 16/Jul/21

Commented by phally last updated on 16/Jul/21

$$\:\:\mathrm{help}\:\mathrm{me}? \\ $$
Commented by tabata last updated on 16/Jul/21
![A)let:y^6 =2x+1⇒3y^5 dy=dx (A)=∫ ((3y^5 )/(y^4 −y^3 ))dy=3∫ ((y^2 −1+1)/(y−1))dy (A)=3∫ [(y+1)+(1/(y−1))]dy=3(y^2 /2)+3y+3 ln∣y−1∣+C replase y by ((2x+1))^(1/6) ∴(A)=∫ (dx/( (((2x+1)^2 ))^(1/3) −(√(2x+1))))=(3/2)((2x+1))^(1/3) +3((2x+1))^(1/6) +3 ln∣((2x+1))^(1/6) −1∣+C ⟨M:T⟩](https://www.tinkutara.com/question/Q146932.png)
$$\left.{A}\right){let}:{y}^{\mathrm{6}} =\mathrm{2}{x}+\mathrm{1}\Rightarrow\mathrm{3}{y}^{\mathrm{5}} {dy}={dx} \\ $$$$ \\ $$$$\left({A}\right)=\int\:\:\frac{\mathrm{3}{y}^{\mathrm{5}} }{{y}^{\mathrm{4}} −{y}^{\mathrm{3}} }{dy}=\mathrm{3}\int\:\frac{{y}^{\mathrm{2}} −\mathrm{1}+\mathrm{1}}{{y}−\mathrm{1}}{dy} \\ $$$$ \\ $$$$\left({A}\right)=\mathrm{3}\int\:\left[\left({y}+\mathrm{1}\right)+\frac{\mathrm{1}}{{y}−\mathrm{1}}\right]{dy}=\mathrm{3}\frac{{y}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{3}{y}+\mathrm{3}\:{ln}\mid{y}−\mathrm{1}\mid+{C} \\ $$$$ \\ $$$${replase}\:{y}\:{by}\:\sqrt[{\mathrm{6}}]{\mathrm{2}{x}+\mathrm{1}} \\ $$$$ \\ $$$$\therefore\left({A}\right)=\int\:\frac{{dx}}{\:\sqrt[{\mathrm{3}}]{\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} }−\sqrt{\mathrm{2}{x}+\mathrm{1}}}=\frac{\mathrm{3}}{\mathrm{2}}\sqrt[{\mathrm{3}}]{\mathrm{2}{x}+\mathrm{1}}+\mathrm{3}\sqrt[{\mathrm{6}}]{\mathrm{2}{x}+\mathrm{1}}+\mathrm{3}\:{ln}\mid\sqrt[{\mathrm{6}}]{\mathrm{2}{x}+\mathrm{1}}−\mathrm{1}\mid+{C} \\ $$$$\langle{M}:{T}\rangle \\ $$$$ \\ $$
Commented by tabata last updated on 16/Jul/21
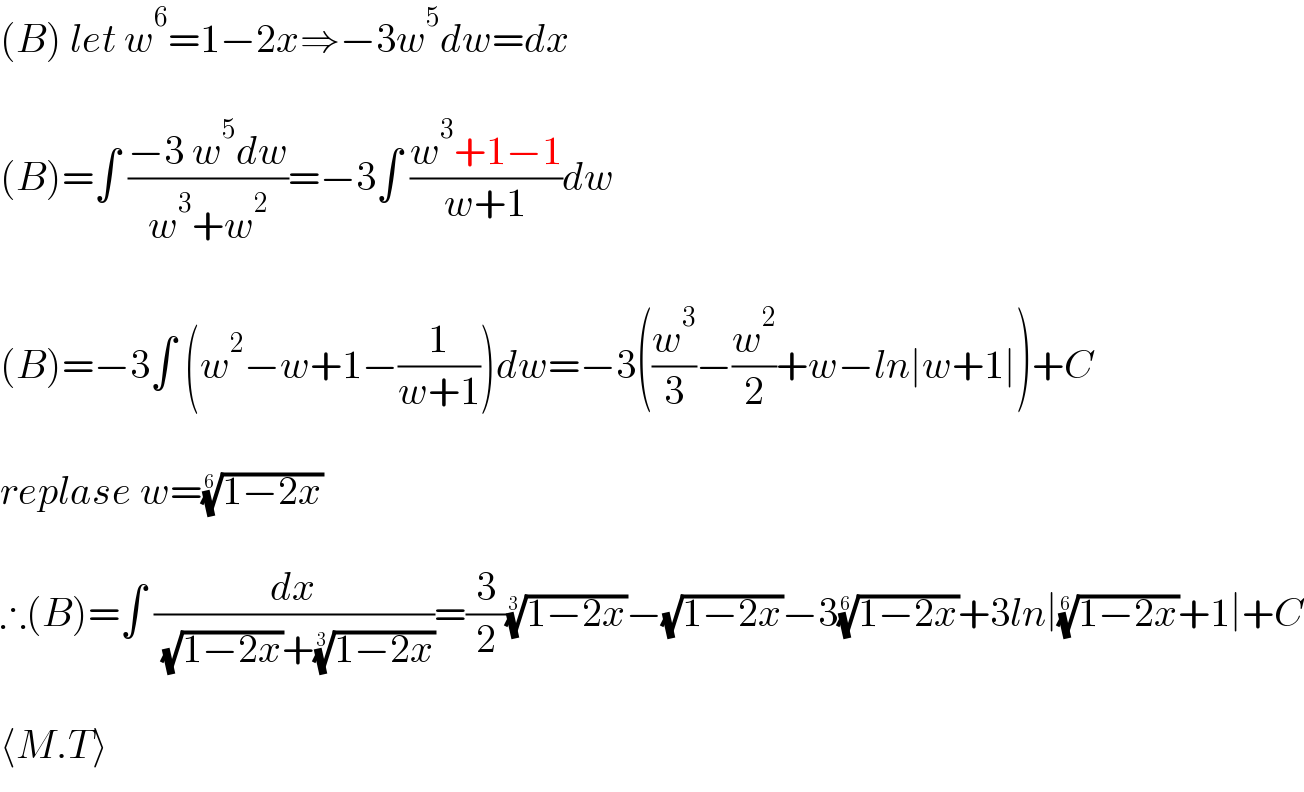
$$\left({B}\right)\:{let}\:{w}^{\mathrm{6}} =\mathrm{1}−\mathrm{2}{x}\Rightarrow−\mathrm{3}{w}^{\mathrm{5}} {dw}={dx} \\ $$$$ \\ $$$$\left({B}\right)=\int\:\frac{−\mathrm{3}\:{w}^{\mathrm{5}} {dw}}{{w}^{\mathrm{3}} +{w}^{\mathrm{2}} }=−\mathrm{3}\int\:\frac{{w}^{\mathrm{3}} +\mathrm{1}−\mathrm{1}}{{w}+\mathrm{1}}{dw} \\ $$$$ \\ $$$$\left({B}\right)=−\mathrm{3}\int\:\left({w}^{\mathrm{2}} −{w}+\mathrm{1}−\frac{\mathrm{1}}{{w}+\mathrm{1}}\right){dw}=−\mathrm{3}\left(\frac{{w}^{\mathrm{3}} }{\mathrm{3}}−\frac{{w}^{\mathrm{2}} }{\mathrm{2}}+{w}−{ln}\mid{w}+\mathrm{1}\mid\right)+{C} \\ $$$$ \\ $$$${replase}\:{w}=\sqrt[{\mathrm{6}}]{\mathrm{1}−\mathrm{2}{x}} \\ $$$$ \\ $$$$\therefore\left({B}\right)=\int\:\frac{{dx}}{\:\sqrt{\mathrm{1}−\mathrm{2}{x}}+\sqrt[{\mathrm{3}}]{\mathrm{1}−\mathrm{2}{x}}}=\frac{\mathrm{3}}{\mathrm{2}}\sqrt[{\mathrm{3}}]{\mathrm{1}−\mathrm{2}{x}}−\sqrt{\mathrm{1}−\mathrm{2}{x}}−\mathrm{3}\sqrt[{\mathrm{6}}]{\mathrm{1}−\mathrm{2}{x}}+\mathrm{3}{ln}\mid\sqrt[{\mathrm{6}}]{\mathrm{1}−\mathrm{2}{x}}+\mathrm{1}\mid+{C} \\ $$$$ \\ $$$$\langle{M}.{T}\rangle \\ $$
Commented by phally last updated on 16/Jul/21

$$\mathrm{thank}\:\mathrm{youw} \\ $$
Commented by tabata last updated on 16/Jul/21

$${you}\:{are}\:{welcome} \\ $$
Answered by behi834171 last updated on 16/Jul/21
![A. let: 2x+1=t^6 ⇒t=(2x+1)^(1/6) ,dx=3t^5 dt ⇒A=∫(( 3t^5 dt)/(t^4 −t^3 ))=∫(( 3t^2 dt)/(t−1))=∫(( 3(t^2 −1)+3)/(t−1))dt= =∫3[t+1+(1/(t−1))]dt= =3[(1/2)t^2 +t+ln∣t−1∣+const.= =(3/2)((2x+1))^(1/3) +3((2x+1))^(1/6) +3ln∣[((2x+1))^(1/6) −1]∣+C .■](https://www.tinkutara.com/question/Q146978.png)
$${A}. \\ $$$${let}:\:\mathrm{2}\boldsymbol{{x}}+\mathrm{1}=\boldsymbol{{t}}^{\mathrm{6}} \Rightarrow\boldsymbol{{t}}=\left(\mathrm{2}\boldsymbol{{x}}+\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{6}}} ,{dx}=\mathrm{3}{t}^{\mathrm{5}} {dt} \\ $$$$\Rightarrow{A}=\int\frac{\:\:\:\:\mathrm{3}{t}^{\mathrm{5}} {dt}}{{t}^{\mathrm{4}} −{t}^{\mathrm{3}} }=\int\frac{\:\:\mathrm{3}{t}^{\mathrm{2}} {dt}}{{t}−\mathrm{1}}=\int\frac{\:\:\mathrm{3}\left({t}^{\mathrm{2}} −\mathrm{1}\right)+\mathrm{3}}{{t}−\mathrm{1}}{dt}= \\ $$$$=\int\mathrm{3}\left[{t}+\mathrm{1}+\frac{\mathrm{1}}{{t}−\mathrm{1}}\right]{dt}= \\ $$$$=\mathrm{3}\left[\frac{\mathrm{1}}{\mathrm{2}}{t}^{\mathrm{2}} +{t}+{ln}\mid{t}−\mathrm{1}\mid+{const}.=\right. \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}\sqrt[{\mathrm{3}}]{\mathrm{2}\boldsymbol{{x}}+\mathrm{1}}+\mathrm{3}\sqrt[{\mathrm{6}}]{\mathrm{2}\boldsymbol{{x}}+\mathrm{1}}+\mathrm{3}\boldsymbol{{ln}}\mid\left[\sqrt[{\mathrm{6}}]{\mathrm{2}\boldsymbol{{x}}+\mathrm{1}}−\mathrm{1}\right]\mid+\boldsymbol{{C}}\:\:.\blacksquare \\ $$
