Question Number 132398 by bramlexs22 last updated on 14/Feb/21
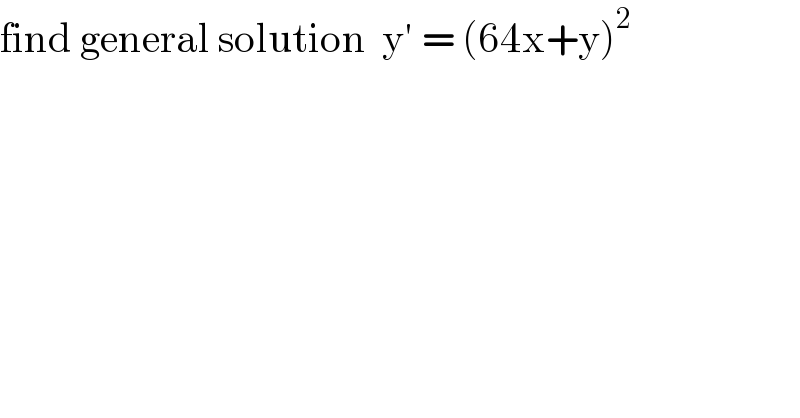
$$\mathrm{find}\:\mathrm{general}\:\mathrm{solution}\:\:\mathrm{y}'\:=\:\left(\mathrm{64x}+\mathrm{y}\right)^{\mathrm{2}} \: \\ $$
Answered by EDWIN88 last updated on 14/Feb/21
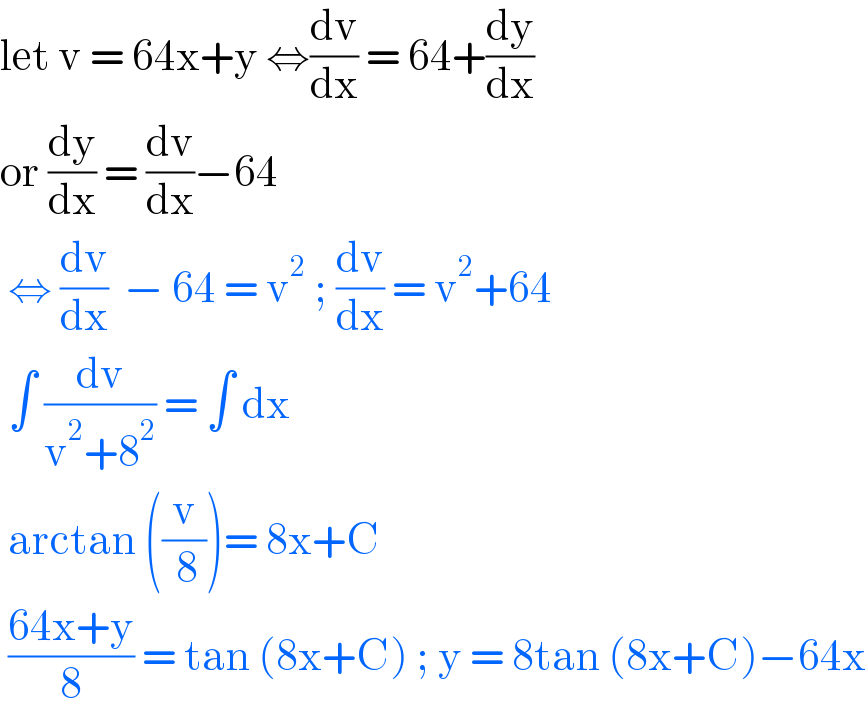
$$\mathrm{let}\:\mathrm{v}\:=\:\mathrm{64x}+\mathrm{y}\:\Leftrightarrow\frac{\mathrm{dv}}{\mathrm{dx}}\:=\:\mathrm{64}+\frac{\mathrm{dy}}{\mathrm{dx}} \\ $$$$\mathrm{or}\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\frac{\mathrm{dv}}{\mathrm{dx}}−\mathrm{64}\: \\ $$$$\:\Leftrightarrow\:\frac{\mathrm{dv}}{\mathrm{dx}}\:\:−\:\mathrm{64}\:=\:\mathrm{v}^{\mathrm{2}} \:;\:\frac{\mathrm{dv}}{\mathrm{dx}}\:=\:\mathrm{v}^{\mathrm{2}} +\mathrm{64}\: \\ $$$$\:\int\:\frac{\mathrm{dv}}{\mathrm{v}^{\mathrm{2}} +\mathrm{8}^{\mathrm{2}} }\:=\:\int\:\mathrm{dx}\: \\ $$$$\:\mathrm{arctan}\:\left(\frac{\mathrm{v}}{\:\mathrm{8}}\right)=\:\mathrm{8x}+\mathrm{C} \\ $$$$\:\frac{\mathrm{64x}+\mathrm{y}}{\mathrm{8}}\:=\:\mathrm{tan}\:\left(\mathrm{8x}+\mathrm{C}\right)\:;\:\mathrm{y}\:=\:\mathrm{8tan}\:\left(\mathrm{8x}+\mathrm{C}\right)−\mathrm{64x} \\ $$
