Question Number 15972 by icyfalcon999 last updated on 16/Jun/17
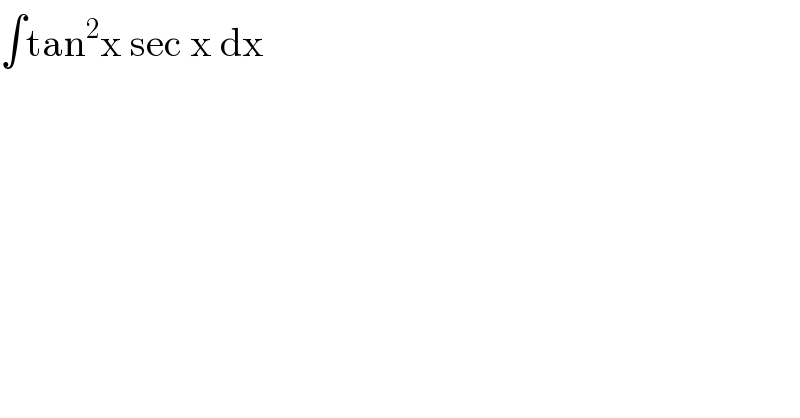
$$\int\mathrm{tan}^{\mathrm{2}} \mathrm{x}\:\mathrm{sec}\:\mathrm{x}\:\mathrm{dx}\: \\ $$
Commented by tawa tawa last updated on 16/Jun/17
![∫tan^2 x secx dx From the trigonometry identity: tan^2 x = sec^2 x − 1 = ∫(sec^2 x − 1)secx dx = ∫(sec^3 x − secx) dx = ∫sec^3 x dx − ∫secx dx = ∫secx(sec^2 x) dx − [∫secx dx] Using integration by part on ∫secx(sec^2 x) dx let u = secx, du = secxtanx dx let dv = sec^2 x, v = tanx ∴ ∫udv = uv − ∫vdu = secx tanx − ∫tan^2 x secx − [∫secx dx] Set it as the original original integral ∫tan^2 x secx dx ∫tan^2 x secx dx = secx tanx − ∫tan^2 x secx − ∫secx ∫tan^2 x secx dx + ∫tan^2 x secx = secx tanx − ∫secx ∴ 2∫tan^2 x secx = secx tanx − ∫secx ∴ ∫tan^2 x secx = ((secx tanx − ∫secx)/2) ∴ ∫tan^2 x secx = ((secx tanx − ln(secx + tanx))/2) + C](https://www.tinkutara.com/question/Q15974.png)
$$\int\mathrm{tan}^{\mathrm{2}} \mathrm{x}\:\mathrm{secx}\:\mathrm{dx} \\ $$$$\mathrm{From}\:\mathrm{the}\:\mathrm{trigonometry}\:\mathrm{identity}:\:\mathrm{tan}^{\mathrm{2}} \mathrm{x}\:=\:\mathrm{sec}^{\mathrm{2}} \mathrm{x}\:−\:\mathrm{1} \\ $$$$\:=\:\int\left(\mathrm{sec}^{\mathrm{2}} \mathrm{x}\:−\:\mathrm{1}\right)\mathrm{secx}\:\mathrm{dx} \\ $$$$=\:\int\left(\mathrm{sec}^{\mathrm{3}} \mathrm{x}\:−\:\mathrm{secx}\right)\:\mathrm{dx} \\ $$$$=\:\int\mathrm{sec}^{\mathrm{3}} \mathrm{x}\:\mathrm{dx}\:−\:\int\mathrm{secx}\:\mathrm{dx} \\ $$$$=\:\int\mathrm{secx}\left(\mathrm{sec}^{\mathrm{2}} \mathrm{x}\right)\:\mathrm{dx}\:−\:\left[\int\mathrm{secx}\:\mathrm{dx}\right] \\ $$$$\mathrm{Using}\:\mathrm{integration}\:\mathrm{by}\:\mathrm{part}\:\mathrm{on}\:\int\mathrm{secx}\left(\mathrm{sec}^{\mathrm{2}} \mathrm{x}\right)\:\mathrm{dx} \\ $$$$\mathrm{let}\:\:\mathrm{u}\:=\:\mathrm{secx},\:\:\mathrm{du}\:=\:\mathrm{secxtanx}\:\mathrm{dx} \\ $$$$\mathrm{let}\:\:\mathrm{dv}\:=\:\mathrm{sec}^{\mathrm{2}} \mathrm{x},\:\:\mathrm{v}\:=\:\mathrm{tanx} \\ $$$$\therefore\:\int\mathrm{udv}\:=\:\mathrm{uv}\:−\:\int\mathrm{vdu} \\ $$$$=\:\mathrm{secx}\:\mathrm{tanx}\:−\:\int\mathrm{tan}^{\mathrm{2}} \mathrm{x}\:\mathrm{secx}\:−\:\left[\int\mathrm{secx}\:\mathrm{dx}\right] \\ $$$$\mathrm{Set}\:\mathrm{it}\:\mathrm{as}\:\mathrm{the}\:\mathrm{original}\:\mathrm{original}\:\mathrm{integral}\:\:\int\mathrm{tan}^{\mathrm{2}} \mathrm{x}\:\mathrm{secx}\:\mathrm{dx} \\ $$$$\int\mathrm{tan}^{\mathrm{2}} \mathrm{x}\:\mathrm{secx}\:\mathrm{dx}\:=\:\mathrm{secx}\:\mathrm{tanx}\:−\:\int\mathrm{tan}^{\mathrm{2}} \mathrm{x}\:\mathrm{secx}\:−\:\int\mathrm{secx} \\ $$$$\int\mathrm{tan}^{\mathrm{2}} \mathrm{x}\:\mathrm{secx}\:\mathrm{dx}\:+\:\int\mathrm{tan}^{\mathrm{2}} \mathrm{x}\:\mathrm{secx}\:=\:\mathrm{secx}\:\mathrm{tanx}\:−\:\int\mathrm{secx} \\ $$$$\therefore\:\mathrm{2}\int\mathrm{tan}^{\mathrm{2}} \mathrm{x}\:\mathrm{secx}\:=\:\mathrm{secx}\:\mathrm{tanx}\:−\:\int\mathrm{secx} \\ $$$$\therefore\:\int\mathrm{tan}^{\mathrm{2}} \mathrm{x}\:\mathrm{secx}\:=\:\frac{\mathrm{secx}\:\mathrm{tanx}\:−\:\int\mathrm{secx}}{\mathrm{2}} \\ $$$$\therefore\:\int\mathrm{tan}^{\mathrm{2}} \mathrm{x}\:\mathrm{secx}\:=\:\frac{\mathrm{secx}\:\mathrm{tanx}\:−\:\mathrm{ln}\left(\mathrm{secx}\:+\:\mathrm{tanx}\right)}{\mathrm{2}}\:+\:\mathrm{C} \\ $$
