Question Number 147119 by mathdanisur last updated on 18/Jul/21
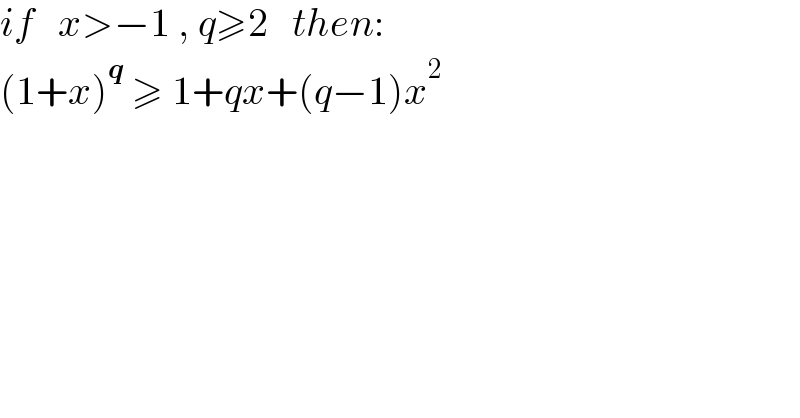
$${if}\:\:\:{x}>−\mathrm{1}\:,\:{q}\geqslant\mathrm{2}\:\:\:{then}: \\ $$$$\left(\mathrm{1}+{x}\right)^{\boldsymbol{{q}}} \:\geqslant\:\mathrm{1}+{qx}+\left({q}−\mathrm{1}\right){x}^{\mathrm{2}} \\ $$
Answered by mindispower last updated on 18/Jul/21
![1+qx+(q−1)x^2 =(q−1)(x+1)(x+(1/(q−1))) ⇔(((1+x)^(q−1) )/(q−1))≥x+(1/(q−1)) ⇔(1+x)^(q−1) ≥(q−1)x+1 f(x)=(1+x)^(q−1) −((q−1)x+1) f′(x)=(q−1)((1+x)^(q−2) −1) f′(x)>0,x∈[0,∞[ f′(x)<0,x∈]−1,0[ ⇒∀x∈]−1,+∞[ ⇒f(x)≥f(0)=(1+0)^(q−1) −1=0 ⇒f(x)≥0⇔(1+x)^(q−1) ≥(q−1)x+1](https://www.tinkutara.com/question/Q147185.png)
$$ \\ $$$$\mathrm{1}+{qx}+\left({q}−\mathrm{1}\right){x}^{\mathrm{2}} =\left({q}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)\left({x}+\frac{\mathrm{1}}{{q}−\mathrm{1}}\right) \\ $$$$\Leftrightarrow\frac{\left(\mathrm{1}+{x}\right)^{{q}−\mathrm{1}} }{{q}−\mathrm{1}}\geqslant{x}+\frac{\mathrm{1}}{{q}−\mathrm{1}} \\ $$$$\Leftrightarrow\left(\mathrm{1}+{x}\right)^{{q}−\mathrm{1}} \geqslant\left({q}−\mathrm{1}\right){x}+\mathrm{1} \\ $$$${f}\left({x}\right)=\left(\mathrm{1}+{x}\right)^{{q}−\mathrm{1}} −\left(\left({q}−\mathrm{1}\right){x}+\mathrm{1}\right) \\ $$$${f}'\left({x}\right)=\left({q}−\mathrm{1}\right)\left(\left(\mathrm{1}+{x}\right)^{{q}−\mathrm{2}} −\mathrm{1}\right) \\ $$$${f}'\left({x}\right)>\mathrm{0},{x}\in\left[\mathrm{0},\infty\left[\right.\right. \\ $$$$\left.{f}'\left({x}\right)<\mathrm{0},{x}\in\right]−\mathrm{1},\mathrm{0}\left[\right. \\ $$$$\left.\Rightarrow\forall{x}\in\right]−\mathrm{1},+\infty\left[\right. \\ $$$$\Rightarrow{f}\left({x}\right)\geqslant{f}\left(\mathrm{0}\right)=\left(\mathrm{1}+\mathrm{0}\right)^{{q}−\mathrm{1}} −\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{f}\left({x}\right)\geqslant\mathrm{0}\Leftrightarrow\left(\mathrm{1}+{x}\right)^{{q}−\mathrm{1}} \geqslant\left({q}−\mathrm{1}\right){x}+\mathrm{1} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by mathdanisur last updated on 19/Jul/21

$${thank}\:{you}\:{Ser} \\ $$
Answered by mathmax by abdo last updated on 19/Jul/21
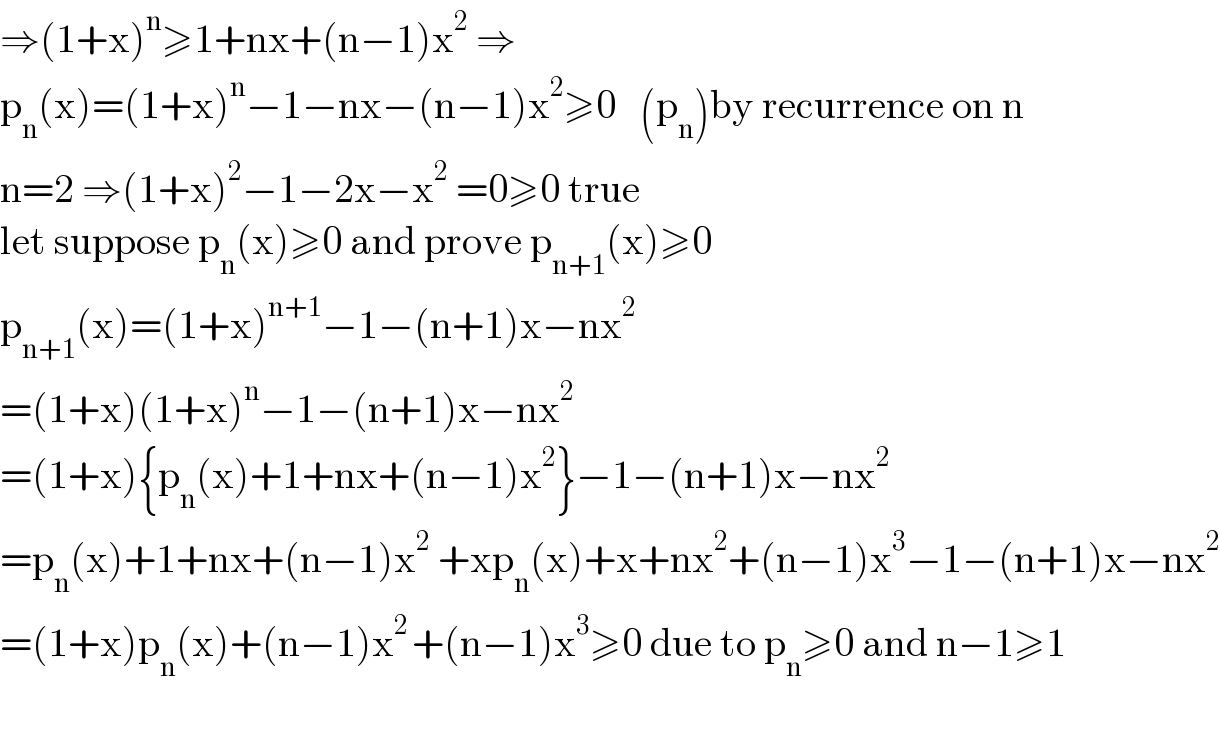
$$\Rightarrow\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{n}} \geqslant\mathrm{1}+\mathrm{nx}+\left(\mathrm{n}−\mathrm{1}\right)\mathrm{x}^{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{p}_{\mathrm{n}} \left(\mathrm{x}\right)=\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{n}} −\mathrm{1}−\mathrm{nx}−\left(\mathrm{n}−\mathrm{1}\right)\mathrm{x}^{\mathrm{2}} \geqslant\mathrm{0}\:\:\:\left(\mathrm{p}_{\mathrm{n}} \right)\mathrm{by}\:\mathrm{recurrence}\:\mathrm{on}\:\mathrm{n} \\ $$$$\mathrm{n}=\mathrm{2}\:\Rightarrow\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{2}} −\mathrm{1}−\mathrm{2x}−\mathrm{x}^{\mathrm{2}} \:=\mathrm{0}\geqslant\mathrm{0}\:\mathrm{true} \\ $$$$\mathrm{let}\:\mathrm{suppose}\:\mathrm{p}_{\mathrm{n}} \left(\mathrm{x}\right)\geqslant\mathrm{0}\:\mathrm{and}\:\mathrm{prove}\:\mathrm{p}_{\mathrm{n}+\mathrm{1}} \left(\mathrm{x}\right)\geqslant\mathrm{0} \\ $$$$\mathrm{p}_{\mathrm{n}+\mathrm{1}} \left(\mathrm{x}\right)=\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{n}+\mathrm{1}} −\mathrm{1}−\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}−\mathrm{nx}^{\mathrm{2}} \\ $$$$=\left(\mathrm{1}+\mathrm{x}\right)\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{n}} −\mathrm{1}−\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}−\mathrm{nx}^{\mathrm{2}} \\ $$$$=\left(\mathrm{1}+\mathrm{x}\right)\left\{\mathrm{p}_{\mathrm{n}} \left(\mathrm{x}\right)+\mathrm{1}+\mathrm{nx}+\left(\mathrm{n}−\mathrm{1}\right)\mathrm{x}^{\mathrm{2}} \right\}−\mathrm{1}−\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}−\mathrm{nx}^{\mathrm{2}} \\ $$$$=\mathrm{p}_{\mathrm{n}} \left(\mathrm{x}\right)+\mathrm{1}+\mathrm{nx}+\left(\mathrm{n}−\mathrm{1}\right)\mathrm{x}^{\mathrm{2}} \:+\mathrm{xp}_{\mathrm{n}} \left(\mathrm{x}\right)+\mathrm{x}+\mathrm{nx}^{\mathrm{2}} +\left(\mathrm{n}−\mathrm{1}\right)\mathrm{x}^{\mathrm{3}} −\mathrm{1}−\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}−\mathrm{nx}^{\mathrm{2}} \\ $$$$=\left(\mathrm{1}+\mathrm{x}\right)\mathrm{p}_{\mathrm{n}} \left(\mathrm{x}\right)+\left(\mathrm{n}−\mathrm{1}\right)\mathrm{x}^{\mathrm{2}\:} +\left(\mathrm{n}−\mathrm{1}\right)\mathrm{x}^{\mathrm{3}} \geqslant\mathrm{0}\:\mathrm{due}\:\mathrm{to}\:\mathrm{p}_{\mathrm{n}} \geqslant\mathrm{0}\:\mathrm{and}\:\mathrm{n}−\mathrm{1}\geqslant\mathrm{1} \\ $$$$ \\ $$
Commented by mathdanisur last updated on 19/Jul/21

$${thank}\:{you}\:{Ser} \\ $$
