Question Number 147310 by mnjuly1970 last updated on 19/Jul/21
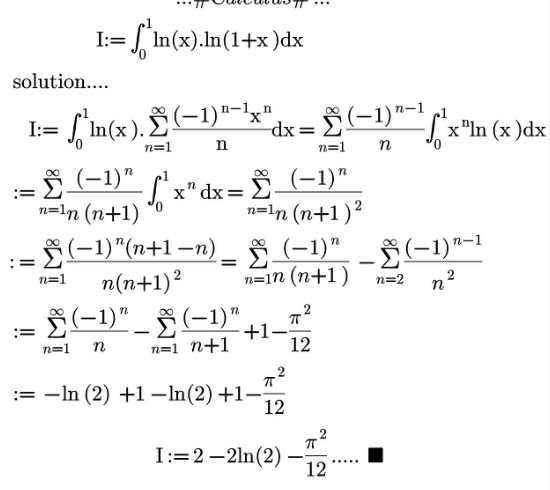
Commented by Tawa11 last updated on 03/Aug/21

$$\mathrm{Great} \\ $$
Answered by qaz last updated on 20/Jul/21
![∫_0 ^1 ln(x)∙ln(1+x)dx =xln(x)∙ln(1+x)∣_0 ^1 −∫_0 ^1 x(((ln(1+x))/x)+((lnx)/(1+x)))dx =−∫_0 ^1 (ln(1+x)+(1−(1/(1+x)))lnxdx =−[(1+x)ln(1+x)−(1+x)]_0 ^1 −∫_0 ^1 lnxdx+∫_0 ^1 ((lnx)/(1+x))dx =1−2ln2−[xlnx−x]_0 ^1 +ln(1+x)lnx∣_0 ^1 −∫_0 ^1 ((ln(1+x))/x)dx =2−2ln2−(π^2 /(12))](https://www.tinkutara.com/question/Q147341.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{x}\right)\centerdot\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\mathrm{dx} \\ $$$$=\mathrm{xln}\left(\mathrm{x}\right)\centerdot\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\mid_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}\left(\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}}+\frac{\mathrm{lnx}}{\mathrm{1}+\mathrm{x}}\right)\mathrm{dx} \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)+\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}}\right)\mathrm{lnxdx}\right. \\ $$$$=−\left[\left(\mathrm{1}+\mathrm{x}\right)\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)−\left(\mathrm{1}+\mathrm{x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{lnxdx}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{lnx}}{\mathrm{1}+\mathrm{x}}\mathrm{dx} \\ $$$$=\mathrm{1}−\mathrm{2ln2}−\left[\mathrm{xlnx}−\mathrm{x}\right]_{\mathrm{0}} ^{\mathrm{1}} +\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\mathrm{lnx}\mid_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx} \\ $$$$=\mathrm{2}−\mathrm{2ln2}−\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$
