Question Number 16240 by tawa tawa last updated on 19/Jun/17

Commented by tawa tawa last updated on 19/Jun/17

$$\mathrm{please}\:\mathrm{help}. \\ $$
Answered by ajfour last updated on 19/Jun/17
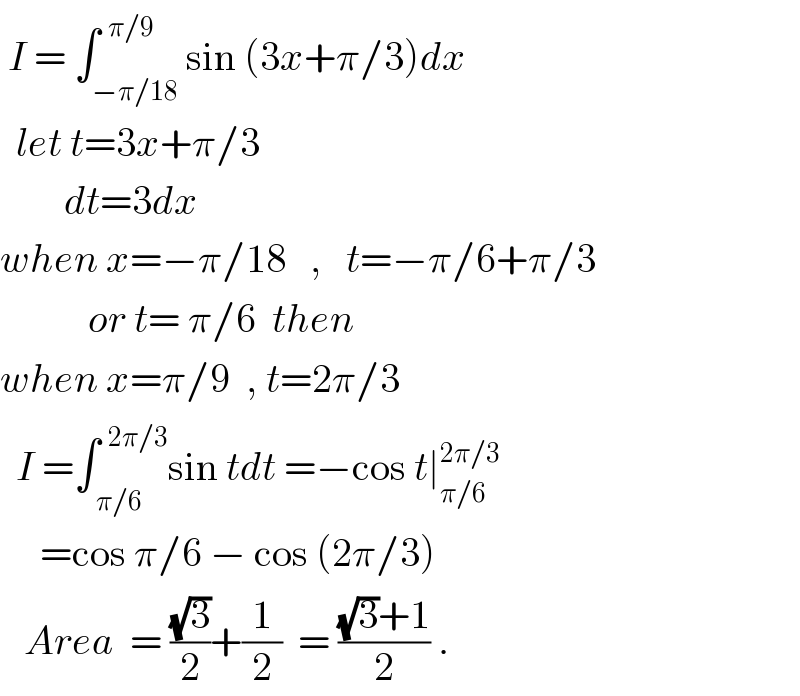
$$\:{I}\:=\:\int_{−\pi/\mathrm{18}} ^{\:\:\pi/\mathrm{9}} \mathrm{sin}\:\left(\mathrm{3}{x}+\pi/\mathrm{3}\right){dx} \\ $$$$\:\:{let}\:{t}=\mathrm{3}{x}+\pi/\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:{dt}=\mathrm{3}{dx}\: \\ $$$${when}\:{x}=−\pi/\mathrm{18}\:\:\:,\:\:\:{t}=−\pi/\mathrm{6}+\pi/\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{or}\:{t}=\:\pi/\mathrm{6}\:\:{then} \\ $$$${when}\:{x}=\pi/\mathrm{9}\:\:,\:{t}=\mathrm{2}\pi/\mathrm{3} \\ $$$$\:\:{I}\:=\int_{\:\pi/\mathrm{6}} ^{\:\:\mathrm{2}\pi/\mathrm{3}} \mathrm{sin}\:{tdt}\:=−\mathrm{cos}\:{t}\mid_{\pi/\mathrm{6}} ^{\mathrm{2}\pi/\mathrm{3}} \\ $$$$\:\:\:\:\:=\mathrm{cos}\:\pi/\mathrm{6}\:−\:\mathrm{cos}\:\left(\mathrm{2}\pi/\mathrm{3}\right) \\ $$$$\:\:\:{Area}\:\:=\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\:\:=\:\frac{\sqrt{\mathrm{3}}+\mathrm{1}}{\mathrm{2}}\:. \\ $$
Commented by tawa tawa last updated on 20/Jun/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by ajfour last updated on 19/Jun/17
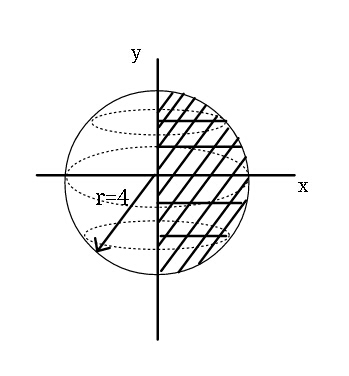
Commented by ajfour last updated on 19/Jun/17
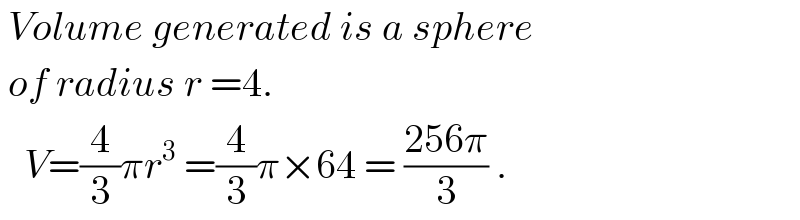
$$\:{Volume}\:{generated}\:{is}\:{a}\:{sphere} \\ $$$$\:{of}\:{radius}\:{r}\:=\mathrm{4}. \\ $$$$\:\:\:{V}=\frac{\mathrm{4}}{\mathrm{3}}\pi{r}^{\mathrm{3}} \:=\frac{\mathrm{4}}{\mathrm{3}}\pi×\mathrm{64}\:=\:\frac{\mathrm{256}\pi}{\mathrm{3}}\:. \\ $$
