Question Number 147349 by bramlexs22 last updated on 20/Jul/21
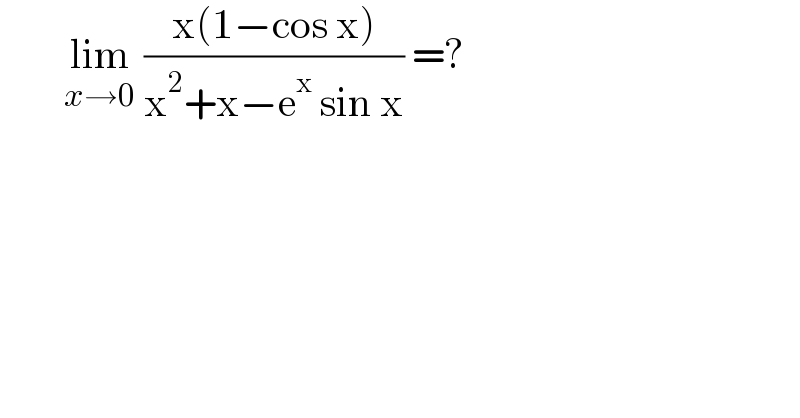
$$\:\:\:\:\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{x}\left(\mathrm{1}−\mathrm{cos}\:\mathrm{x}\right)}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\mathrm{e}^{\mathrm{x}} \:\mathrm{sin}\:\mathrm{x}}\:=? \\ $$
Commented by bramlexs22 last updated on 20/Jul/21

Commented by EDWIN88 last updated on 20/Jul/21
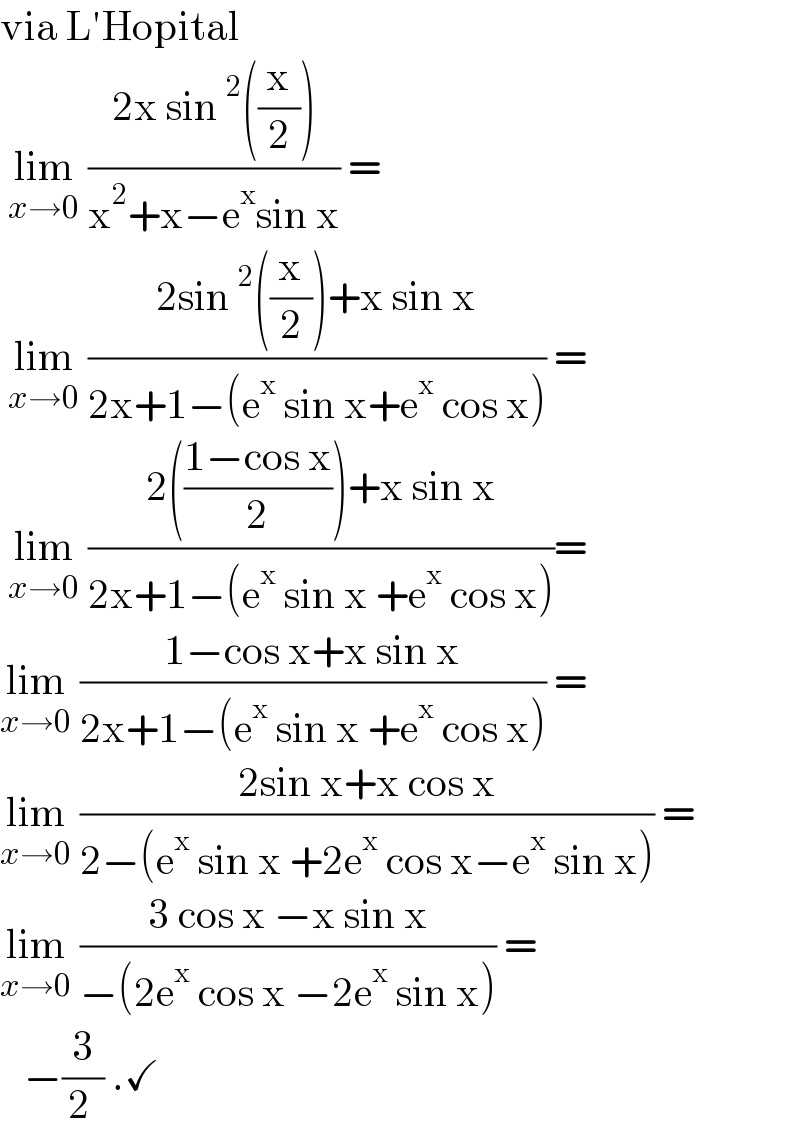
$$\mathrm{via}\:\mathrm{L}'\mathrm{Hopital}\: \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2x}\:\mathrm{sin}\:^{\mathrm{2}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\mathrm{e}^{\mathrm{x}} \mathrm{sin}\:\mathrm{x}}\:= \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2sin}\:^{\mathrm{2}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)+\mathrm{x}\:\mathrm{sin}\:\mathrm{x}}{\mathrm{2x}+\mathrm{1}−\left(\mathrm{e}^{\mathrm{x}} \:\mathrm{sin}\:\mathrm{x}+\mathrm{e}^{\mathrm{x}} \:\mathrm{cos}\:\mathrm{x}\right)}\:= \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}\left(\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{x}}{\mathrm{2}}\right)+\mathrm{x}\:\mathrm{sin}\:\mathrm{x}}{\mathrm{2x}+\mathrm{1}−\left(\mathrm{e}^{\mathrm{x}} \:\mathrm{sin}\:\mathrm{x}\:+\mathrm{e}^{\mathrm{x}} \:\mathrm{cos}\:\mathrm{x}\right)}= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{x}+\mathrm{x}\:\mathrm{sin}\:\mathrm{x}}{\mathrm{2x}+\mathrm{1}−\left(\mathrm{e}^{\mathrm{x}} \:\mathrm{sin}\:\mathrm{x}\:+\mathrm{e}^{\mathrm{x}} \:\mathrm{cos}\:\mathrm{x}\right)}\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2sin}\:\mathrm{x}+\mathrm{x}\:\mathrm{cos}\:\mathrm{x}}{\mathrm{2}−\left(\mathrm{e}^{\mathrm{x}} \:\mathrm{sin}\:\mathrm{x}\:+\mathrm{2e}^{\mathrm{x}} \:\mathrm{cos}\:\mathrm{x}−\mathrm{e}^{\mathrm{x}} \:\mathrm{sin}\:\mathrm{x}\right)}\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{3}\:\mathrm{cos}\:\mathrm{x}\:−\mathrm{x}\:\mathrm{sin}\:\mathrm{x}}{−\left(\mathrm{2e}^{\mathrm{x}} \:\mathrm{cos}\:\mathrm{x}\:−\mathrm{2e}^{\mathrm{x}} \:\mathrm{sin}\:\mathrm{x}\right)}\:= \\ $$$$\:\:\:−\frac{\mathrm{3}}{\mathrm{2}\:}\:.\checkmark \\ $$
Answered by ArielVyny last updated on 20/Jul/21
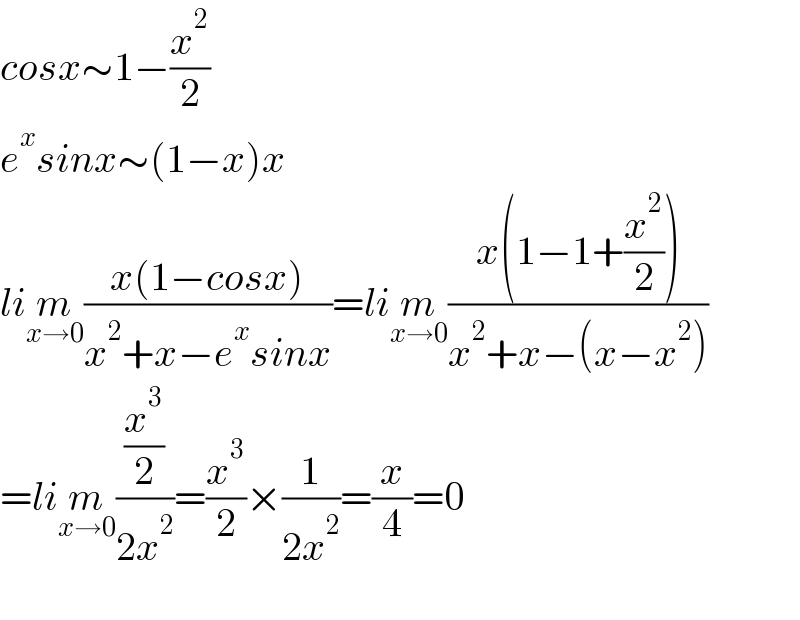
$${cosx}\sim\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${e}^{{x}} {sinx}\sim\left(\mathrm{1}−{x}\right){x} \\ $$$${li}\underset{{x}\rightarrow\mathrm{0}} {{m}}\frac{{x}\left(\mathrm{1}−{cosx}\right)}{{x}^{\mathrm{2}} +{x}−{e}^{{x}} {sinx}}={li}\underset{{x}\rightarrow\mathrm{0}} {{m}}\frac{{x}\left(\mathrm{1}−\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)}{{x}^{\mathrm{2}} +{x}−\left({x}−{x}^{\mathrm{2}} \right)} \\ $$$$={li}\underset{{x}\rightarrow\mathrm{0}} {{m}}\frac{\frac{{x}^{\mathrm{3}} }{\mathrm{2}}}{\mathrm{2}{x}^{\mathrm{2}} }=\frac{{x}^{\mathrm{3}} }{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }=\frac{{x}}{\mathrm{4}}=\mathrm{0} \\ $$$$ \\ $$
Commented by bramlexs22 last updated on 20/Jul/21

$$\mathrm{false}\: \\ $$
Answered by mathmax by abdo last updated on 20/Jul/21
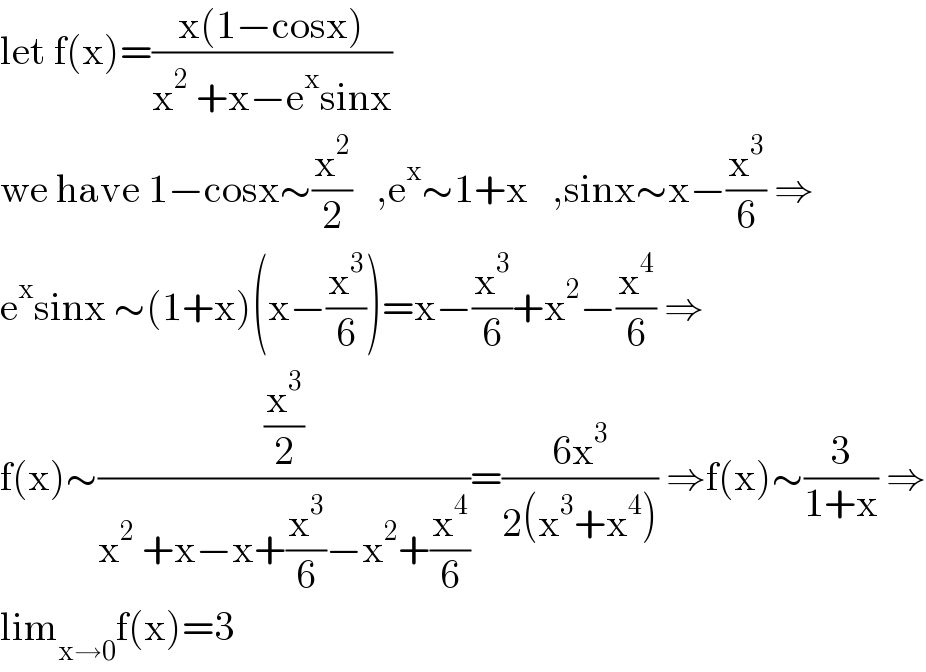
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{x}\left(\mathrm{1}−\mathrm{cosx}\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}−\mathrm{e}^{\mathrm{x}} \mathrm{sinx}} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{1}−\mathrm{cosx}\sim\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\:\:\:,\mathrm{e}^{\mathrm{x}} \sim\mathrm{1}+\mathrm{x}\:\:\:,\mathrm{sinx}\sim\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}\:\Rightarrow \\ $$$$\mathrm{e}^{\mathrm{x}} \mathrm{sinx}\:\sim\left(\mathrm{1}+\mathrm{x}\right)\left(\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}\right)=\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}+\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{6}}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\sim\frac{\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{2}}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}−\mathrm{x}+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}−\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{6}}}=\frac{\mathrm{6x}^{\mathrm{3}} }{\mathrm{2}\left(\mathrm{x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{4}} \right)}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\sim\frac{\mathrm{3}}{\mathrm{1}+\mathrm{x}}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \mathrm{f}\left(\mathrm{x}\right)=\mathrm{3} \\ $$
Commented by liberty last updated on 20/Jul/21
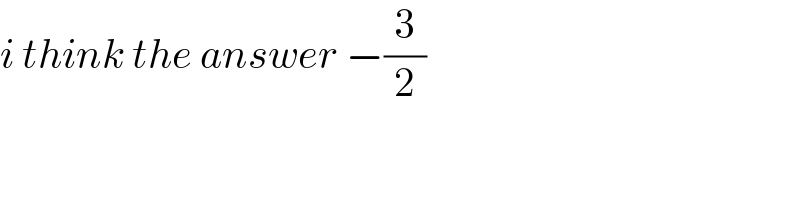
$${i}\:{think}\:{the}\:{answer}\:−\frac{\mathrm{3}}{\mathrm{2}} \\ $$
