Question Number 147412 by vvvv last updated on 20/Jul/21
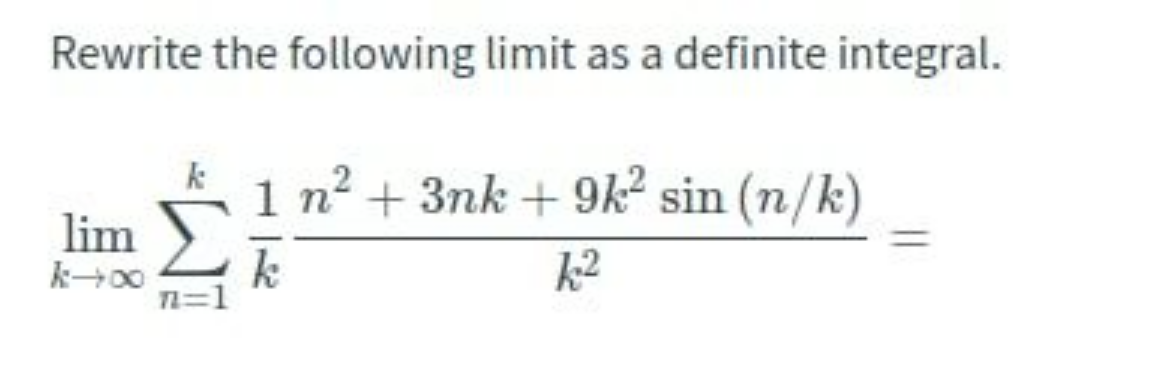
Answered by puissant last updated on 21/Jul/21
![=lim_(k→∞) (1/k)Σ_(n=1) ^k ((n^2 +3nk+9k^2 sin((n/k)))/k^2 ) =lim_(k→∞) (1/k)Σ_(n=1) ^k [((n/k))^2 +3((n/k))+9sin((n/k)) Riemann integral.. ⇒ lim_(k→∞) U_k = ∫_0 ^( 1) x^2 +3x+9sin(x) dx =(1/3)[x^3 ]_0 ^1 +(3/2)[x^2 ]_0 ^1 −9[cos(x)]_0 ^1 =(1/3)+(3/2)−9cos(1)+9 ⇒lim_(k→∞ ) U_k =((65)/6)−9cos(1)..](https://www.tinkutara.com/question/Q147446.png)
$$={lim}_{{k}\rightarrow\infty} \frac{\mathrm{1}}{{k}}\underset{{n}=\mathrm{1}} {\overset{{k}} {\sum}}\frac{{n}^{\mathrm{2}} +\mathrm{3}{nk}+\mathrm{9}{k}^{\mathrm{2}} {sin}\left(\frac{{n}}{{k}}\right)}{{k}^{\mathrm{2}} } \\ $$$$={lim}_{{k}\rightarrow\infty} \frac{\mathrm{1}}{{k}}\underset{{n}=\mathrm{1}} {\overset{{k}} {\sum}}\left[\left(\frac{{n}}{{k}}\right)^{\mathrm{2}} +\mathrm{3}\left(\frac{{n}}{{k}}\right)+\mathrm{9}{sin}\left(\frac{{n}}{{k}}\right)\right. \\ $$$${Riemann}\:{integral}.. \\ $$$$\Rightarrow\:{lim}_{{k}\rightarrow\infty} {U}_{{k}} =\:\int_{\mathrm{0}} ^{\:\mathrm{1}} {x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{9}{sin}\left({x}\right)\:{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left[{x}^{\mathrm{3}} \right]_{\mathrm{0}} ^{\mathrm{1}} +\frac{\mathrm{3}}{\mathrm{2}}\left[{x}^{\mathrm{2}} \right]_{\mathrm{0}} ^{\mathrm{1}} −\mathrm{9}\left[{cos}\left({x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{9}{cos}\left(\mathrm{1}\right)+\mathrm{9} \\ $$$$\Rightarrow{lim}_{{k}\rightarrow\infty\:} {U}_{{k}} =\frac{\mathrm{65}}{\mathrm{6}}−\mathrm{9}{cos}\left(\mathrm{1}\right).. \\ $$
