Question Number 82042 by ajfour last updated on 17/Feb/20

Commented by ajfour last updated on 17/Feb/20

$${Find}\:{ratio}\:{of}\:{side}\:{lengths}\:{of} \\ $$$${outer}\:{equilateral}\:\bigtriangleup{KLM}\:{to} \\ $$$${that}\:{of}\:{inner}\:{equilateral}\:\bigtriangleup{PQR}. \\ $$
Commented by mr W last updated on 19/Feb/20
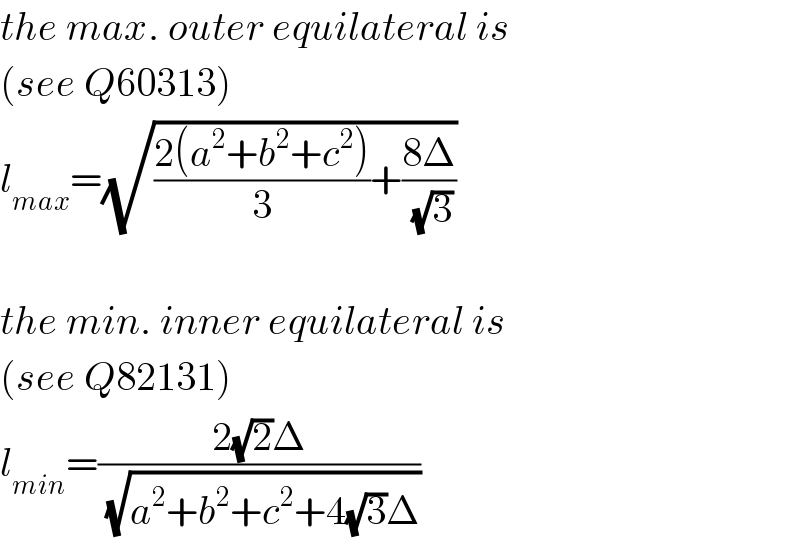
$${the}\:{max}.\:{outer}\:{equilateral}\:{is} \\ $$$$\left({see}\:{Q}\mathrm{60313}\right) \\ $$$${l}_{{max}} =\sqrt{\frac{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)}{\mathrm{3}}+\frac{\mathrm{8}\Delta}{\:\sqrt{\mathrm{3}}}} \\ $$$$ \\ $$$${the}\:{min}.\:{inner}\:{equilateral}\:{is} \\ $$$$\left({see}\:{Q}\mathrm{82131}\right) \\ $$$${l}_{{min}} =\frac{\mathrm{2}\sqrt{\mathrm{2}}\Delta}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +\mathrm{4}\sqrt{\mathrm{3}}\Delta}} \\ $$
Commented by ajfour last updated on 17/Feb/20
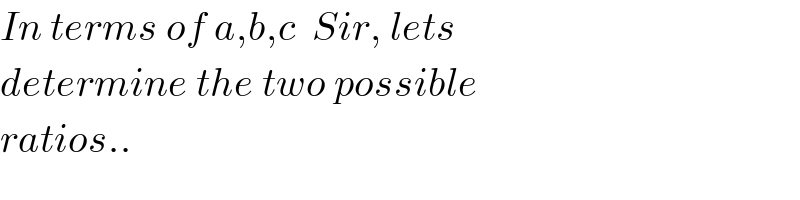
$${In}\:{terms}\:{of}\:{a},{b},{c}\:\:{Sir},\:{lets}\: \\ $$$${determine}\:{the}\:{two}\:{possible} \\ $$$${ratios}.. \\ $$
Commented by ajfour last updated on 25/Feb/20
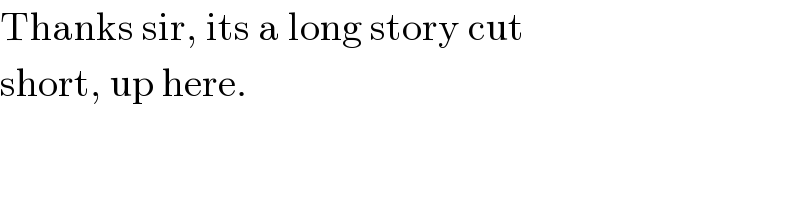
$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{its}\:\mathrm{a}\:\mathrm{long}\:\mathrm{story}\:\mathrm{cut} \\ $$$$\mathrm{short},\:\mathrm{up}\:\mathrm{here}. \\ $$
