Solve-simultaneously-x-2-y-2-61-equation-i-x-3-y-3-91-equation-ii-

Question Number 16600 by tawa tawa last updated on 24/Jun/17

$$\mathrm{Solve}\:\mathrm{simultaneously} \\ $$$$\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{y}^{\mathrm{2}} \:=\:\mathrm{61}\:\:\:\:\:\:\:\:\:…………..\:\mathrm{equation}\:\left(\mathrm{i}\right) \\ $$$$\mathrm{x}^{\mathrm{3}} \:−\:\mathrm{y}^{\mathrm{3}} \:=\:\mathrm{91}\:\:\:\:\:\:\:\:\:…………..\:\mathrm{equation}\:\left(\mathrm{ii}\right) \\ $$

Commented by prakash jain last updated on 24/Jun/17

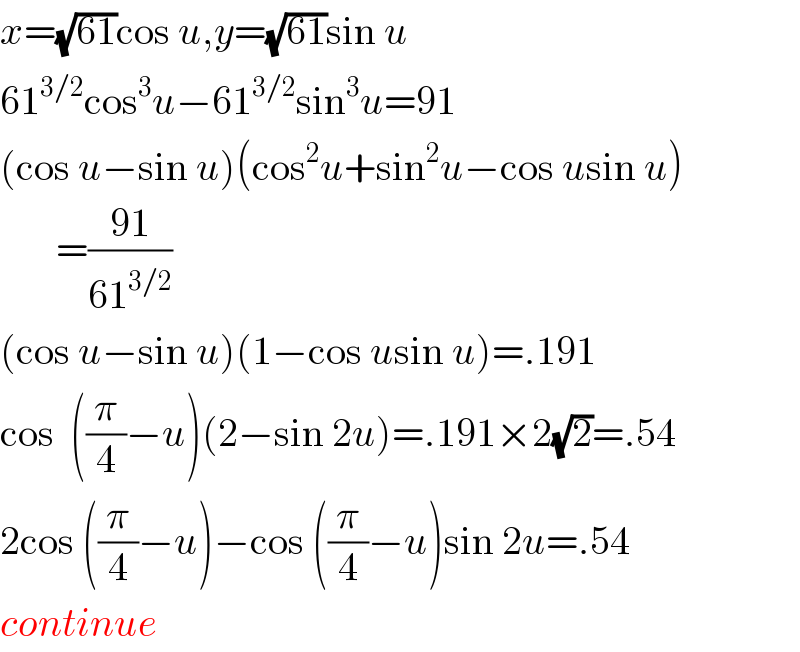
x=(√(61))cos u,y=(√(61))sin u 61^(3/2) cos^3 u−61^(3/2) sin^3 u=91 (cos u−sin u)(cos^2 u+sin^2 u−cos usin u) =((91)/(61^(3/2) )) (cos u−sin u)(1−cos usin u)=.191 cos ((π/4)−u)(2−sin 2u)=.191×2(√2)=.54 2cos ((π/4)−u)−cos ((π/4)−u)sin 2u=.54 continue

$${x}=\sqrt{\mathrm{61}}\mathrm{cos}\:{u},{y}=\sqrt{\mathrm{61}}\mathrm{sin}\:{u} \\ $$$$\mathrm{61}^{\mathrm{3}/\mathrm{2}} \mathrm{cos}^{\mathrm{3}} {u}−\mathrm{61}^{\mathrm{3}/\mathrm{2}} \mathrm{sin}^{\mathrm{3}} {u}=\mathrm{91} \\ $$$$\left(\mathrm{cos}\:{u}−\mathrm{sin}\:{u}\right)\left(\mathrm{cos}^{\mathrm{2}} {u}+\mathrm{sin}^{\mathrm{2}} {u}−\mathrm{cos}\:{u}\mathrm{sin}\:{u}\right) \\ $$$$\:\:\:\:\:\:\:=\frac{\mathrm{91}}{\mathrm{61}^{\mathrm{3}/\mathrm{2}} } \\ $$$$\left(\mathrm{cos}\:{u}−\mathrm{sin}\:{u}\right)\left(\mathrm{1}−\mathrm{cos}\:{u}\mathrm{sin}\:{u}\right)=.\mathrm{191} \\ $$$$\mathrm{cos}\:\:\left(\frac{\pi}{\mathrm{4}}−{u}\right)\left(\mathrm{2}−\mathrm{sin}\:\mathrm{2}{u}\right)=.\mathrm{191}×\mathrm{2}\sqrt{\mathrm{2}}=.\mathrm{54} \\ $$$$\mathrm{2cos}\:\left(\frac{\pi}{\mathrm{4}}−{u}\right)−\mathrm{cos}\:\left(\frac{\pi}{\mathrm{4}}−{u}\right)\mathrm{sin}\:\mathrm{2}{u}=.\mathrm{54} \\ $$$${continue} \\ $$

Commented by tawa tawa last updated on 24/Jun/17

$$\mathrm{Am}\:\mathrm{with}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Commented by Tinkutara last updated on 24/Jun/17

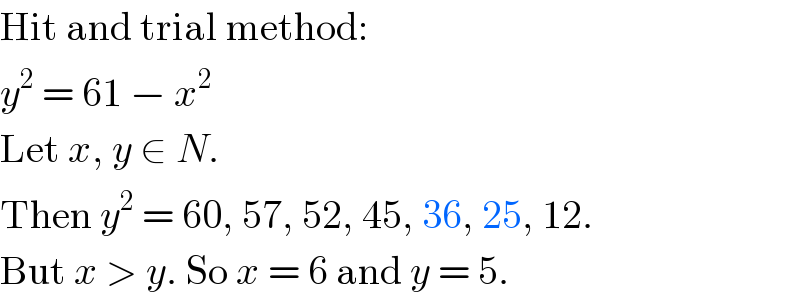
Hit and trial method: y^2 = 61 − x^2 Let x, y ∈ N. Then y^2 = 60, 57, 52, 45, 36, 25, 12. But x > y. So x = 6 and y = 5.

$$\mathrm{Hit}\:\mathrm{and}\:\mathrm{trial}\:\mathrm{method}: \\ $$$${y}^{\mathrm{2}} \:=\:\mathrm{61}\:−\:{x}^{\mathrm{2}} \\ $$$$\mathrm{Let}\:{x},\:{y}\:\in\:{N}. \\ $$$$\mathrm{Then}\:{y}^{\mathrm{2}} \:=\:\mathrm{60},\:\mathrm{57},\:\mathrm{52},\:\mathrm{45},\:\mathrm{36},\:\mathrm{25},\:\mathrm{12}. \\ $$$$\mathrm{But}\:{x}\:>\:{y}.\:\mathrm{So}\:{x}\:=\:\mathrm{6}\:\mathrm{and}\:{y}\:=\:\mathrm{5}. \\ $$

Commented by tawa tawa last updated on 24/Jun/17

$$\mathrm{Am}\:\mathrm{with}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 26/Jun/17

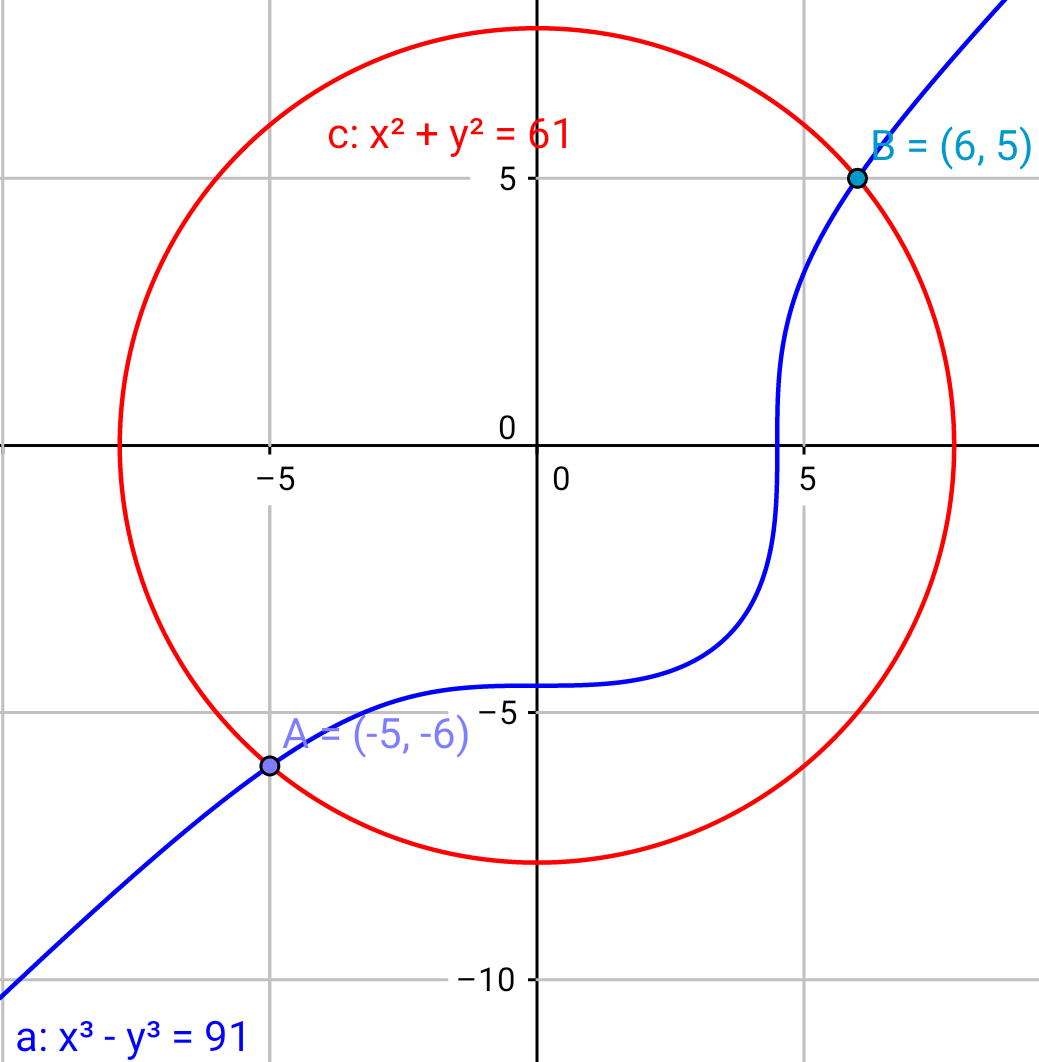
Commented by mrW1 last updated on 26/Jun/17

$$\mathrm{geogebra}\:\mathrm{is}\:\mathrm{very}\:\mathrm{powerful}! \\ $$

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 26/Jun/17

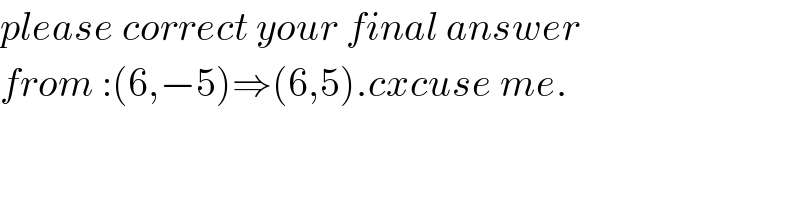
please correct your final answer from :(6,−5)⇒(6,5).cxcuse me.

$${please}\:{correct}\:{your}\:{final}\:{answer} \\ $$$${from}\::\left(\mathrm{6},−\mathrm{5}\right)\Rightarrow\left(\mathrm{6},\mathrm{5}\right).{cxcuse}\:{me}. \\ $$

Commented by mrW1 last updated on 26/Jun/17

$$\mathrm{certainly}\:\mathrm{you}\:\mathrm{are}\:\mathrm{right}.\:\mathrm{thanks}! \\ $$

Answered by mrW1 last updated on 26/Jun/17

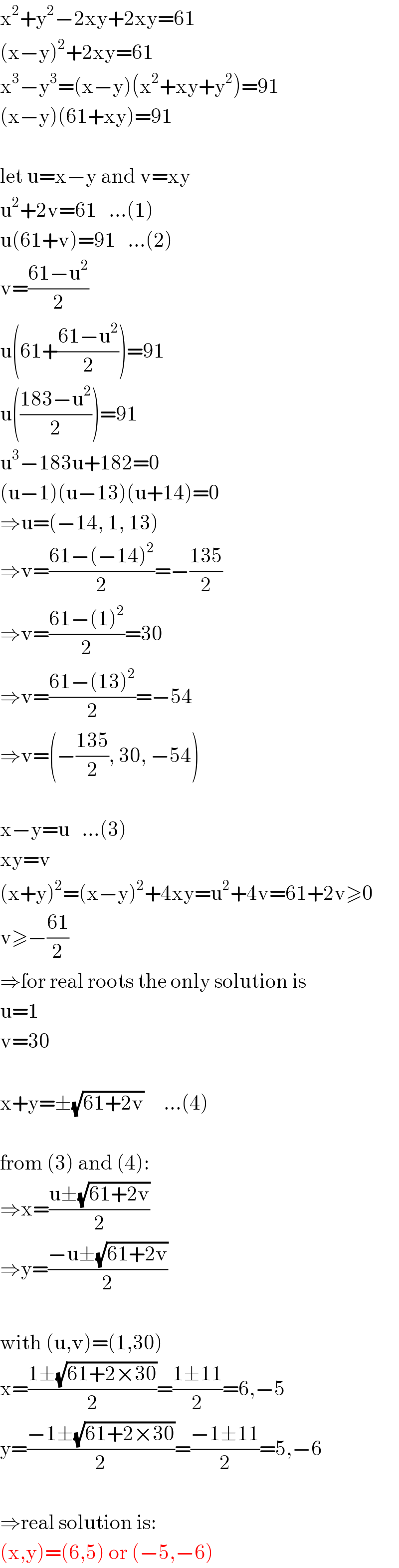
x^2 +y^2 −2xy+2xy=61 (x−y)^2 +2xy=61 x^3 −y^3 =(x−y)(x^2 +xy+y^2 )=91 (x−y)(61+xy)=91 let u=x−y and v=xy u^2 +2v=61 ...(1) u(61+v)=91 ...(2) v=((61−u^2 )/2) u(61+((61−u^2 )/2))=91 u(((183−u^2 )/2))=91 u^3 −183u+182=0 (u−1)(u−13)(u+14)=0 ⇒u=(−14, 1, 13) ⇒v=((61−(−14)^2 )/2)=−((135)/2) ⇒v=((61−(1)^2 )/2)=30 ⇒v=((61−(13)^2 )/2)=−54 ⇒v=(−((135)/2), 30, −54) x−y=u ...(3) xy=v (x+y)^2 =(x−y)^2 +4xy=u^2 +4v=61+2v≥0 v≥−((61)/2) ⇒for real roots the only solution is u=1 v=30 x+y=±(√(61+2v)) ...(4) from (3) and (4): ⇒x=((u±(√(61+2v)))/2) ⇒y=((−u±(√(61+2v)))/2) with (u,v)=(1,30) x=((1±(√(61+2×30)))/2)=((1±11)/2)=6,−5 y=((−1±(√(61+2×30)))/2)=((−1±11)/2)=5,−6 ⇒real solution is: (x,y)=(6,5) or (−5,−6)

$$\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} −\mathrm{2xy}+\mathrm{2xy}=\mathrm{61} \\ $$$$\left(\mathrm{x}−\mathrm{y}\right)^{\mathrm{2}} +\mathrm{2xy}=\mathrm{61} \\ $$$$\mathrm{x}^{\mathrm{3}} −\mathrm{y}^{\mathrm{3}} =\left(\mathrm{x}−\mathrm{y}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{xy}+\mathrm{y}^{\mathrm{2}} \right)=\mathrm{91} \\ $$$$\left(\mathrm{x}−\mathrm{y}\right)\left(\mathrm{61}+\mathrm{xy}\right)=\mathrm{91} \\ $$$$ \\ $$$$\mathrm{let}\:\mathrm{u}=\mathrm{x}−\mathrm{y}\:\mathrm{and}\:\mathrm{v}=\mathrm{xy} \\ $$$$\mathrm{u}^{\mathrm{2}} +\mathrm{2v}=\mathrm{61}\:\:\:…\left(\mathrm{1}\right) \\ $$$$\mathrm{u}\left(\mathrm{61}+\mathrm{v}\right)=\mathrm{91}\:\:\:…\left(\mathrm{2}\right) \\ $$$$\mathrm{v}=\frac{\mathrm{61}−\mathrm{u}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\mathrm{u}\left(\mathrm{61}+\frac{\mathrm{61}−\mathrm{u}^{\mathrm{2}} }{\mathrm{2}}\right)=\mathrm{91} \\ $$$$\mathrm{u}\left(\frac{\mathrm{183}−\mathrm{u}^{\mathrm{2}} }{\mathrm{2}}\right)=\mathrm{91} \\ $$$$\mathrm{u}^{\mathrm{3}} −\mathrm{183u}+\mathrm{182}=\mathrm{0} \\ $$$$\left(\mathrm{u}−\mathrm{1}\right)\left(\mathrm{u}−\mathrm{13}\right)\left(\mathrm{u}+\mathrm{14}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{u}=\left(−\mathrm{14},\:\mathrm{1},\:\mathrm{13}\right) \\ $$$$\Rightarrow\mathrm{v}=\frac{\mathrm{61}−\left(−\mathrm{14}\right)^{\mathrm{2}} }{\mathrm{2}}=−\frac{\mathrm{135}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{v}=\frac{\mathrm{61}−\left(\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}}=\mathrm{30} \\ $$$$\Rightarrow\mathrm{v}=\frac{\mathrm{61}−\left(\mathrm{13}\right)^{\mathrm{2}} }{\mathrm{2}}=−\mathrm{54} \\ $$$$\Rightarrow\mathrm{v}=\left(−\frac{\mathrm{135}}{\mathrm{2}},\:\mathrm{30},\:−\mathrm{54}\right) \\ $$$$ \\ $$$$\mathrm{x}−\mathrm{y}=\mathrm{u}\:\:\:…\left(\mathrm{3}\right) \\ $$$$\mathrm{xy}=\mathrm{v} \\ $$$$\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{2}} =\left(\mathrm{x}−\mathrm{y}\right)^{\mathrm{2}} +\mathrm{4xy}=\mathrm{u}^{\mathrm{2}} +\mathrm{4v}=\mathrm{61}+\mathrm{2v}\geqslant\mathrm{0} \\ $$$$\mathrm{v}\geqslant−\frac{\mathrm{61}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{for}\:\mathrm{real}\:\mathrm{roots}\:\mathrm{the}\:\mathrm{only}\:\mathrm{solution}\:\mathrm{is}\: \\ $$$$\mathrm{u}=\mathrm{1} \\ $$$$\mathrm{v}=\mathrm{30} \\ $$$$ \\ $$$$\mathrm{x}+\mathrm{y}=\pm\sqrt{\mathrm{61}+\mathrm{2v}}\:\:\:\:\:…\left(\mathrm{4}\right) \\ $$$$ \\ $$$$\mathrm{from}\:\left(\mathrm{3}\right)\:\mathrm{and}\:\left(\mathrm{4}\right): \\ $$$$\Rightarrow\mathrm{x}=\frac{\mathrm{u}\pm\sqrt{\mathrm{61}+\mathrm{2v}}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{y}=\frac{−\mathrm{u}\pm\sqrt{\mathrm{61}+\mathrm{2v}}}{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{with}\:\left(\mathrm{u},\mathrm{v}\right)=\left(\mathrm{1},\mathrm{30}\right) \\ $$$$\mathrm{x}=\frac{\mathrm{1}\pm\sqrt{\mathrm{61}+\mathrm{2}×\mathrm{30}}}{\mathrm{2}}=\frac{\mathrm{1}\pm\mathrm{11}}{\mathrm{2}}=\mathrm{6},−\mathrm{5} \\ $$$$\mathrm{y}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{61}+\mathrm{2}×\mathrm{30}}}{\mathrm{2}}=\frac{−\mathrm{1}\pm\mathrm{11}}{\mathrm{2}}=\mathrm{5},−\mathrm{6} \\ $$$$ \\ $$$$\Rightarrow\mathrm{real}\:\mathrm{solution}\:\mathrm{is}: \\ $$$$\left(\mathrm{x},\mathrm{y}\right)=\left(\mathrm{6},\mathrm{5}\right)\:\mathrm{or}\:\left(−\mathrm{5},−\mathrm{6}\right) \\ $$

Commented by tawa tawa last updated on 24/Jun/17