Question Number 1395 by Rasheed Soomro last updated on 28/Jul/15

$$\:\:\:\:\:\:\:\:\:\:\mathrm{C}{onsider}\:\boldsymbol{\mathrm{quadrilateral}}\:\boldsymbol{\mathrm{ABCD}}\:\:{same}\:{as}\:{in}\:{Q}\:\mathrm{1378}\:{with}\: \\ $$$${same}\:{conditions}/{restrictions}\:\left({Pl}\:\:{refer}\:\:{the}\:{Question}\:{again}\right). \\ $$$$\:\:\:\:\:\:\:\:\:\:\bullet\:{What}\:{could}\:{be}\:{possible}\:\boldsymbol{\mathrm{minimum}}\:{and}\:\boldsymbol{\mathrm{maximum}}\:\boldsymbol{\mathrm{area}} \\ $$$${of}\:{the}\:{quadrilateral}? \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\bullet{When}\:{qusdrilateral}\:{has}\:\boldsymbol{\mathrm{minimum}}\:\boldsymbol{\mathrm{area}}\:{what}\:{is}\:{the}\:{value}/{s} \\ $$$${of}\:\boldsymbol{{m}}\angle\boldsymbol{\mathrm{A}}?\:{Similarly}\:{what}\:{is}\:{value}/{s}\:\:{of}\:\boldsymbol{{m}}\angle\boldsymbol{\mathrm{A}}\:{in}\:{case}\:{of} \\ $$$$\boldsymbol{\mathrm{maximum}}\:\boldsymbol{\mathrm{area}}? \\ $$$$ \\ $$
Commented by prakash jain last updated on 28/Jul/15
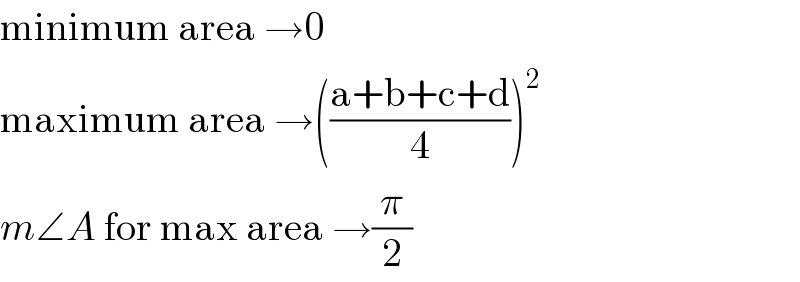
$$\mathrm{minimum}\:\mathrm{area}\:\rightarrow\mathrm{0} \\ $$$$\mathrm{maximum}\:\mathrm{area}\:\rightarrow\left(\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{d}}{\mathrm{4}}\right)^{\mathrm{2}} \\ $$$${m}\angle{A}\:\mathrm{for}\:\mathrm{max}\:\mathrm{area}\:\rightarrow\frac{\pi}{\mathrm{2}} \\ $$
Commented by Rasheed Soomro last updated on 29/Jul/15

$${In}\:{order}\:{to}\:{learn}\:{I}\:{put}\:{my}\:{questions}\:\left({raised}\:{in}\:{my}\:{mind}\right) \\ $$$${before}\:{you}.\:{I}\:{want}\:{to}\:{be}\:{satisfied},\:{so}\:\boldsymbol{\mathrm{Please}}\:\boldsymbol{\mathrm{reply}}. \\ $$$$\:{maximum}\:{area}\rightarrow\left(\frac{\boldsymbol{{a}}+\boldsymbol{{b}}+\boldsymbol{{c}}+\boldsymbol{{d}}}{\mathrm{4}}\right)^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\: \\ $$$$\bullet{You}\:{have}\:{used}\:{symbol}\:'\rightarrow'\:{in}\:{above}.{Does}\:{this}\:{mean}\:'\:{tends}\:{to}\:'\:? \\ $$$$\bullet{Could}\:{we}\:{replace}\:{it}\:{with}\:'='\:{equally}\:? \\ $$$$\bullet{Does}\:{the}\:{above}\:{expression}\:{can}\:{be}\:{used}\:{as}\:{a}\:{formula}\:{for}\: \\ $$$${the}\:{area}\:{a}\:\boldsymbol{\mathrm{quadrilateral}}\:\boldsymbol{\mathrm{having}}\:\boldsymbol{\mathrm{one}}\:\boldsymbol{\mathrm{angle}}\:\boldsymbol{\mathrm{of}}\:\frac{\boldsymbol{\pi}}{\mathrm{2}}\:\boldsymbol{\mathrm{rad}}.\:{If}\:{yes} \\ $$$${then}\:{it}\:{should}\:{be}\:{used}\:{for}\:{area}\:{of}\:{rectangle}\:{of}\:\boldsymbol{\mathrm{x}}\:\:\boldsymbol{\mathrm{by}}\:\:\boldsymbol{\mathrm{y}}\:. \\ $$$${But}\:{above}\:{formula}\:{gives}\:{the}\:{area}\:\left(\frac{{x}+{y}}{\mathrm{2}}\right)\:{instead}\:{of}\:{xy}! \\ $$$${In}\:{other}\:{words}\:: \\ $$$${Being}\:\:{quadrilateral}\:{maximum}\:{area}\:{of}\:{parallelogram}\:{is} \\ $$$${area}\:{of}\:{rectangle}.\:{If}\:{the}\:{dimensions}\:{of}\:\parallel{gram}\:{are} \\ $$$${x}\:{and}\:{y}\:{then}\:{maximum}\:{area}\:{should}\:{be}\:{xy}\:.{But}\:{the}\:{above}\: \\ $$$${formula}\:{gives}\:{the}\:{result}\:\frac{{x}+{y}}{\mathrm{2}}\:! \\ $$$$ \\ $$
Commented by Rasheed Soomro last updated on 29/Jul/15
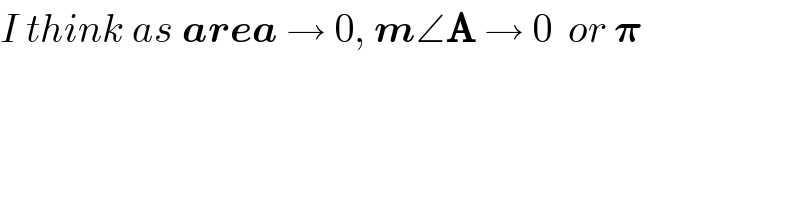
$${I}\:{think}\:{as}\:\boldsymbol{{area}}\:\rightarrow\:\mathrm{0},\:\boldsymbol{{m}}\angle\boldsymbol{\mathrm{A}}\:\rightarrow\:\mathrm{0}\:\:{or}\:\boldsymbol{\pi} \\ $$
Commented by prakash jain last updated on 29/Jul/15
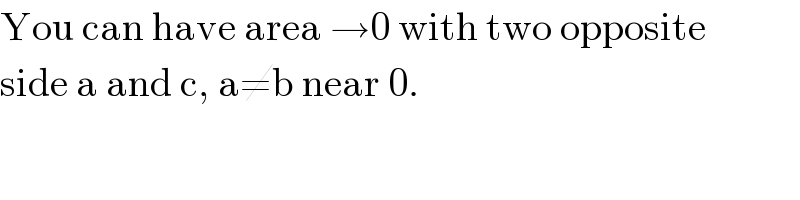
$$\mathrm{You}\:\mathrm{can}\:\mathrm{have}\:\mathrm{area}\:\rightarrow\mathrm{0}\:\mathrm{with}\:\mathrm{two}\:\mathrm{opposite} \\ $$$$\mathrm{side}\:\mathrm{a}\:\mathrm{and}\:\mathrm{c},\:\mathrm{a}\neq\mathrm{b}\:\mathrm{near}\:\mathrm{0}. \\ $$
Commented by Rasheed Ahmad last updated on 31/Jul/15

$${Maximum}\:{area}\:{of}\:{parllelogram} \\ $$$${with}\:{dimensions}\:{x}\:{and}\:{y}\:{is}\:{the} \\ $$$${area}\:{of}\:{rectange}\:{with}\:{same} \\ $$$${dimensions}\:{that}\:{is}\:{xy}\:{if}\:{I}\:{am}\:{right}. \\ $$$${But}\:{your}\:{formula}\:\left(\frac{{a}+{b}+{c}+{d}}{\mathrm{4}}\:\right)^{\mathrm{2}} \\ $$$${gives}\:\left(\frac{{x}+{y}}{\mathrm{2}}\right)^{\mathrm{2}} .{Please}\:{explain}\: \\ $$$${as}\:{I}\:{want}\:{to}\:{learn}\:{from}\:{you}. \\ $$
