Menu Close

Find-the-sum-to-close-form-1-1-2-3-1-4-5-6-1-7-8-9-

Tinku Tara 0 Comments
Pin




Question Number 147877 by Tawa11 last updated on 24/Jul/21
Find the sum to close form. (1/(1.2.3)) + (1/(4.5.6)) + (1/(7.8.9)) + ...
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{to}\:\mathrm{close}\:\mathrm{form}. \\ $$$$\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{1}.\mathrm{2}.\mathrm{3}}\:\:+\:\:\frac{\mathrm{1}}{\mathrm{4}.\mathrm{5}.\mathrm{6}}\:\:\:+\:\:\frac{\mathrm{1}}{\mathrm{7}.\mathrm{8}.\mathrm{9}}\:\:\:+\:\:\:…\:\:\: \\ $$
Commented by Tinku Tara last updated on 24/Jul/21
Welcome back. Tawa. 🙂🙂
$$\mathrm{Welcome}\:\mathrm{back}.\:\mathrm{Tawa}. \\ $$🙂🙂
Commented by Tawa11 last updated on 24/Jul/21
Thank you sir. (⌣^(⌢ . . ⌢) )
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}.\:\:\:\:\:\:\:\:\:\left(\overset{\frown\:\:\:.\:\:\:.\:\:\:\frown} {\smile}\right) \\ $$
Answered by Olaf_Thorendsen last updated on 24/Jul/21
S = Σ_(n=0) ^∞ (1/((3n+1)(3n+2)(3n+3))) S = (1/8)Σ_(n=0) ^∞ (3/((3n+1)(3n+2)))−(5/((3n+2)(3n+3)))+(2/((3n+3)(3n+1))) S = (1/(24))Σ_(n=0) ^∞ (1/((n+(1/3))(n+(2/3))))−(5/(72))Σ_(n=0) ^∞ (1/((n+(2/3))(n+1))) +(1/(36))Σ_(n=0) ^∞ (1/((n+1)(n+(1/3)))) S = (1/(24)).((ψ((2/3))−ψ((1/3)))/((2/3)−(1/3)))−(5/(72)).((ψ(1)−ψ((2/3)))/(1−(2/3))) +(1/(36)).((ψ(1)−ψ((1/3)))/(1−(1/3))) S = (1/8)(ψ((2/3))−ψ((1/3)))−(5/(24))(ψ(1)−ψ((2/3))) +(1/(24))(ψ(1)−ψ((1/3))) S = −(1/6)ψ((1/3))+(1/3)ψ((2/3))−(1/6)ψ(1) • ψ(1−z) = ψ(z)+πcot(πz) ⇒ ψ((2/3)) = ψ((1/3))+πcot((π/3)) ψ((2/3)) = ψ((1/3))+(π/( (√3))) S = (1/6)ψ((1/3))+(π/(3(√3)))−(1/6)ψ(1) • ψ(1) = −γ • ψ((1/3)) = −(π/(2(√3)))−(3/2)ln3−γ S = (1/6)(−(π/(2(√3)))−(3/2)ln3−γ)+(π/(3(√3)))+(γ/6) S = (π/( 4(√3)))−(1/4)ln3
$$\mathrm{S}\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{1}\right)\left(\mathrm{3}{n}+\mathrm{2}\right)\left(\mathrm{3}{n}+\mathrm{3}\right)} \\ $$$$\mathrm{S}\:=\:\frac{\mathrm{1}}{\mathrm{8}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{3}}{\left(\mathrm{3}{n}+\mathrm{1}\right)\left(\mathrm{3}{n}+\mathrm{2}\right)}−\frac{\mathrm{5}}{\left(\mathrm{3}{n}+\mathrm{2}\right)\left(\mathrm{3}{n}+\mathrm{3}\right)}+\frac{\mathrm{2}}{\left(\mathrm{3}{n}+\mathrm{3}\right)\left(\mathrm{3}{n}+\mathrm{1}\right)} \\ $$$$\mathrm{S}\:=\:\frac{\mathrm{1}}{\mathrm{24}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\frac{\mathrm{1}}{\mathrm{3}}\right)\left({n}+\frac{\mathrm{2}}{\mathrm{3}}\right)}−\frac{\mathrm{5}}{\mathrm{72}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\frac{\mathrm{2}}{\mathrm{3}}\right)\left({n}+\mathrm{1}\right)} \\ $$$$+\frac{\mathrm{1}}{\mathrm{36}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)\left({n}+\frac{\mathrm{1}}{\mathrm{3}}\right)} \\ $$$$\mathrm{S}\:=\:\frac{\mathrm{1}}{\mathrm{24}}.\frac{\psi\left(\frac{\mathrm{2}}{\mathrm{3}}\right)−\psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right)}{\frac{\mathrm{2}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}}}−\frac{\mathrm{5}}{\mathrm{72}}.\frac{\psi\left(\mathrm{1}\right)−\psi\left(\frac{\mathrm{2}}{\mathrm{3}}\right)}{\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3}}} \\ $$$$+\frac{\mathrm{1}}{\mathrm{36}}.\frac{\psi\left(\mathrm{1}\right)−\psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right)}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$\mathrm{S}\:=\:\frac{\mathrm{1}}{\mathrm{8}}\left(\psi\left(\frac{\mathrm{2}}{\mathrm{3}}\right)−\psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\right)−\frac{\mathrm{5}}{\mathrm{24}}\left(\psi\left(\mathrm{1}\right)−\psi\left(\frac{\mathrm{2}}{\mathrm{3}}\right)\right) \\ $$$$+\frac{\mathrm{1}}{\mathrm{24}}\left(\psi\left(\mathrm{1}\right)−\psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\right) \\ $$$$\mathrm{S}\:=\:−\frac{\mathrm{1}}{\mathrm{6}}\psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right)+\frac{\mathrm{1}}{\mathrm{3}}\psi\left(\frac{\mathrm{2}}{\mathrm{3}}\right)−\frac{\mathrm{1}}{\mathrm{6}}\psi\left(\mathrm{1}\right) \\ $$$$ \\ $$$$\bullet\:\psi\left(\mathrm{1}−{z}\right)\:=\:\psi\left({z}\right)+\pi\mathrm{cot}\left(\pi{z}\right) \\ $$$$\Rightarrow\:\psi\left(\frac{\mathrm{2}}{\mathrm{3}}\right)\:=\:\psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right)+\pi\mathrm{cot}\left(\frac{\pi}{\mathrm{3}}\right) \\ $$$$\psi\left(\frac{\mathrm{2}}{\mathrm{3}}\right)\:=\:\psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right)+\frac{\pi}{\:\sqrt{\mathrm{3}}} \\ $$$$\mathrm{S}\:=\:\frac{\mathrm{1}}{\mathrm{6}}\psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right)+\frac{\pi}{\mathrm{3}\sqrt{\mathrm{3}}}−\frac{\mathrm{1}}{\mathrm{6}}\psi\left(\mathrm{1}\right) \\ $$$$\bullet\:\psi\left(\mathrm{1}\right)\:=\:−\gamma \\ $$$$\bullet\:\psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\:=\:−\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}}−\frac{\mathrm{3}}{\mathrm{2}}\mathrm{ln3}−\gamma \\ $$$$\mathrm{S}\:=\:\frac{\mathrm{1}}{\mathrm{6}}\left(−\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}}−\frac{\mathrm{3}}{\mathrm{2}}\mathrm{ln3}−\gamma\right)+\frac{\pi}{\mathrm{3}\sqrt{\mathrm{3}}}+\frac{\gamma}{\mathrm{6}} \\ $$$$\mathrm{S}\:=\:\frac{\pi}{\:\mathrm{4}\sqrt{\mathrm{3}}}−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln3} \\ $$
Commented by Tawa11 last updated on 24/Jul/21
Wow, God bless you sir.
$$\mathrm{Wow},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by Tawa11 last updated on 24/Jul/21
Sir, where can I learn summation like this. Please sir prescribe book. I want to study on it too. Thanks sir.
$$\mathrm{Sir},\:\mathrm{where}\:\mathrm{can}\:\mathrm{I}\:\mathrm{learn}\:\mathrm{summation}\:\mathrm{like}\:\mathrm{this}.\:\mathrm{Please}\:\mathrm{sir}\:\mathrm{prescribe}\:\mathrm{book}.\:\mathrm{I}\:\mathrm{want} \\ $$$$\mathrm{to}\:\mathrm{study}\:\mathrm{on}\:\mathrm{it}\:\mathrm{too}.\:\mathrm{Thanks}\:\mathrm{sir}. \\ $$
Commented by Tawa11 last updated on 24/Jul/21
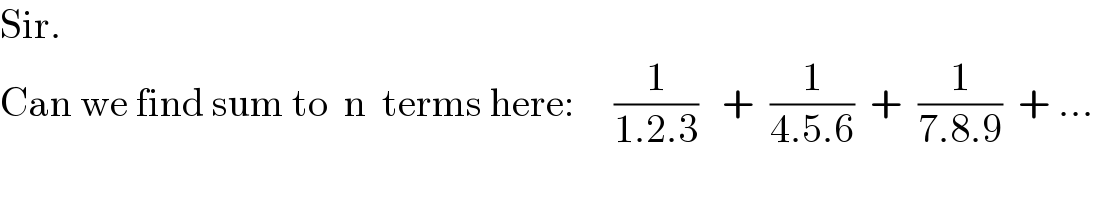
Sir. Can we find sum to n terms here: (1/(1.2.3)) + (1/(4.5.6)) + (1/(7.8.9)) + ...
$$\mathrm{Sir}. \\ $$$$\mathrm{Can}\:\mathrm{we}\:\mathrm{find}\:\mathrm{sum}\:\mathrm{to}\:\:\mathrm{n}\:\:\mathrm{terms}\:\mathrm{here}:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{1}.\mathrm{2}.\mathrm{3}}\:\:\:+\:\:\frac{\mathrm{1}}{\mathrm{4}.\mathrm{5}.\mathrm{6}}\:\:+\:\:\frac{\mathrm{1}}{\mathrm{7}.\mathrm{8}.\mathrm{9}}\:\:+\:… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *