Menu Close

Question-147948

Tinku Tara 0 Comments
Pin




Question Number 147948 by tabata last updated on 24/Jul/21
Commented by tabata last updated on 24/Jul/21
Msr olaf help me please ?
$${Msr}\:{olaf}\:{help}\:{me}\:{please}\:? \\ $$
Answered by Olaf_Thorendsen last updated on 24/Jul/21
h(z) = (1/(z^2 sinhz)) = ((f(z))/z^2 ), ∣z∣ < R The zeros of sinh(z) are {kπi}_(k∈Z) so the highest possible value for R is π. For ∣z∣<π, we have f(z) = (1/(sinhz)) = (1/(z+(z^3 /(3!))+(z^5 /(5!))+(z^7 /(7!))...)) f(z) = (1/z).(1/(1+((z^2 /6)+(z^4 /(120))+(z^6 /(5040))...))) f(z) = (1/z)(1−((z^2 /6)+(z^4 /(120))+(z^6 /(5040))+...)+((z^2 /6)+(z^4 /(120))+(z^6 /(5040))+...)^2 +...) f(z) = (1/z)(1−(z^2 /6)−(z^4 /(120))−(z^6 /(5040))+(z^4 /(36))+(z^6 /(360))...) f(z) = (1/z)(1−(z^2 /6)+((7z^4 )/(360))+((13z^6 )/(5040))+...) ⇒ h(z) = (1/z^3 )−(1/(6z))+((7z)/(360))+((13z^3 )/(5040))+...
$${h}\left({z}\right)\:=\:\frac{\mathrm{1}}{{z}^{\mathrm{2}} \mathrm{sinh}{z}}\:=\:\frac{{f}\left({z}\right)}{{z}^{\mathrm{2}} },\:\mid{z}\mid\:<\:\mathrm{R} \\ $$$$\mathrm{The}\:\mathrm{zeros}\:\mathrm{of}\:\mathrm{sinh}\left({z}\right)\:\mathrm{are}\:\left\{{k}\pi{i}\right\}_{{k}\in\mathbb{Z}} \:\:\mathrm{so} \\ $$$$\mathrm{the}\:\mathrm{highest}\:\mathrm{possible}\:\mathrm{value}\:\mathrm{for}\:\mathrm{R}\:\mathrm{is}\:\pi. \\ $$$$ \\ $$$$\mathrm{For}\:\mid{z}\mid<\pi,\:\mathrm{we}\:\mathrm{have} \\ $$$${f}\left({z}\right)\:=\:\frac{\mathrm{1}}{\mathrm{sinh}{z}}\:=\:\frac{\mathrm{1}}{{z}+\frac{{z}^{\mathrm{3}} }{\mathrm{3}!}+\frac{{z}^{\mathrm{5}} }{\mathrm{5}!}+\frac{{z}^{\mathrm{7}} }{\mathrm{7}!}…} \\ $$$${f}\left({z}\right)\:=\:\frac{\mathrm{1}}{{z}}.\frac{\mathrm{1}}{\mathrm{1}+\left(\frac{{z}^{\mathrm{2}} }{\mathrm{6}}+\frac{{z}^{\mathrm{4}} }{\mathrm{120}}+\frac{{z}^{\mathrm{6}} }{\mathrm{5040}}…\right)} \\ $$$${f}\left({z}\right)\:=\:\frac{\mathrm{1}}{{z}}\left(\mathrm{1}−\left(\frac{{z}^{\mathrm{2}} }{\mathrm{6}}+\frac{{z}^{\mathrm{4}} }{\mathrm{120}}+\frac{{z}^{\mathrm{6}} }{\mathrm{5040}}+…\right)+\left(\frac{{z}^{\mathrm{2}} }{\mathrm{6}}+\frac{{z}^{\mathrm{4}} }{\mathrm{120}}+\frac{{z}^{\mathrm{6}} }{\mathrm{5040}}+…\right)^{\mathrm{2}} +…\right) \\ $$$${f}\left({z}\right)\:=\:\frac{\mathrm{1}}{{z}}\left(\mathrm{1}−\frac{{z}^{\mathrm{2}} }{\mathrm{6}}−\frac{{z}^{\mathrm{4}} }{\mathrm{120}}−\frac{{z}^{\mathrm{6}} }{\mathrm{5040}}+\frac{{z}^{\mathrm{4}} }{\mathrm{36}}+\frac{{z}^{\mathrm{6}} }{\mathrm{360}}…\right) \\ $$$${f}\left({z}\right)\:=\:\frac{\mathrm{1}}{{z}}\left(\mathrm{1}−\frac{{z}^{\mathrm{2}} }{\mathrm{6}}+\frac{\mathrm{7}{z}^{\mathrm{4}} }{\mathrm{360}}+\frac{\mathrm{13}{z}^{\mathrm{6}} }{\mathrm{5040}}+…\right) \\ $$$$\Rightarrow\:{h}\left({z}\right)\:=\:\frac{\mathrm{1}}{{z}^{\mathrm{3}} }−\frac{\mathrm{1}}{\mathrm{6}{z}}+\frac{\mathrm{7}{z}}{\mathrm{360}}+\frac{\mathrm{13}{z}^{\mathrm{3}} }{\mathrm{5040}}+… \\ $$
Commented by tabata last updated on 24/Jul/21
thank you msr olaf
$${thank}\:{you}\:{msr}\:{olaf}\: \\ $$
Commented by tabata last updated on 24/Jul/21
sir can how exactly ((z^2 /6)+(z^4 /(120))+(z^6 /(5040))+...)^2 how me solution please?
$${sir}\:{can}\:{how}\:{exactly}\:\left(\frac{{z}^{\mathrm{2}} }{\mathrm{6}}+\frac{{z}^{\mathrm{4}} }{\mathrm{120}}+\frac{{z}^{\mathrm{6}} }{\mathrm{5040}}+…\right)^{\mathrm{2}} {how}\:{me}\:{solution}\:{please}? \\ $$
Commented by tabata last updated on 24/Jul/21
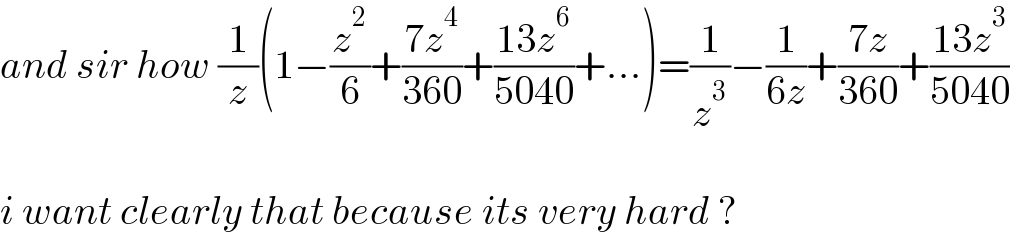
and sir how (1/z)(1−(z^2 /6)+((7z^4 )/(360))+((13z^6 )/(5040))+...)=(1/z^3 )−(1/(6z))+((7z)/(360))+((13z^3 )/(5040)) i want clearly that because its very hard ?
$${and}\:{sir}\:{how}\:\frac{\mathrm{1}}{{z}}\left(\mathrm{1}−\frac{{z}^{\mathrm{2}} }{\mathrm{6}}+\frac{\mathrm{7}{z}^{\mathrm{4}} }{\mathrm{360}}+\frac{\mathrm{13}{z}^{\mathrm{6}} }{\mathrm{5040}}+…\right)=\frac{\mathrm{1}}{{z}^{\mathrm{3}} }−\frac{\mathrm{1}}{\mathrm{6}{z}}+\frac{\mathrm{7}{z}}{\mathrm{360}}+\frac{\mathrm{13}{z}^{\mathrm{3}} }{\mathrm{5040}} \\ $$$$ \\ $$$${i}\:{want}\:{clearly}\:{that}\:{because}\:{its}\:{very}\:{hard}\:? \\ $$
Commented by Olaf_Thorendsen last updated on 24/Jul/21
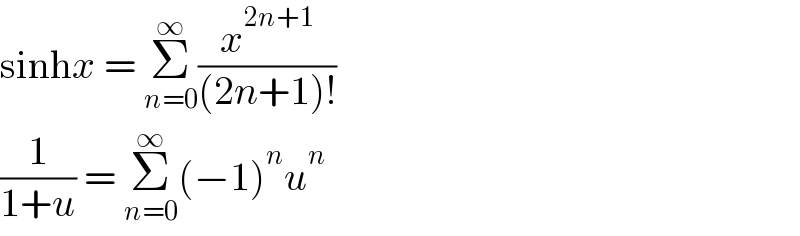
sinhx = Σ_(n=0) ^∞ (x^(2n+1) /((2n+1)!)) (1/(1+u)) = Σ_(n=0) ^∞ (−1)^n u^n
$$\mathrm{sinh}{x}\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{\mathrm{2}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+{u}}\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} {u}^{{n}} \\ $$
Commented by mr W last updated on 24/Jul/21
please recheck sir: i think it should be f(z) = (1/z)(1−(z^2 /6)−(z^4 /(120))−(z^6 /(5040))+(z^4 /(36))+(z^6 /(360))−(z^6 /(216))...) f(z) = (1/z)(1−(z^2 /6)+((7z^4 )/(360))−((31z^6 )/(15120))+...) ⇒ h(z) = (1/z^3 )−(1/(6z))+((7z)/(360))−((31z^3 )/(15120))+...
$${please}\:{recheck}\:{sir}: \\ $$$${i}\:{think}\:{it}\:{should}\:{be} \\ $$$${f}\left({z}\right)\:=\:\frac{\mathrm{1}}{{z}}\left(\mathrm{1}−\frac{{z}^{\mathrm{2}} }{\mathrm{6}}−\frac{{z}^{\mathrm{4}} }{\mathrm{120}}−\frac{{z}^{\mathrm{6}} }{\mathrm{5040}}+\frac{{z}^{\mathrm{4}} }{\mathrm{36}}+\frac{{z}^{\mathrm{6}} }{\mathrm{360}}−\frac{{z}^{\mathrm{6}} }{\mathrm{216}}…\right) \\ $$$${f}\left({z}\right)\:=\:\frac{\mathrm{1}}{{z}}\left(\mathrm{1}−\frac{{z}^{\mathrm{2}} }{\mathrm{6}}+\frac{\mathrm{7}{z}^{\mathrm{4}} }{\mathrm{360}}−\frac{\mathrm{31}{z}^{\mathrm{6}} }{\mathrm{15120}}+…\right) \\ $$$$\Rightarrow\:{h}\left({z}\right)\:=\:\frac{\mathrm{1}}{{z}^{\mathrm{3}} }−\frac{\mathrm{1}}{\mathrm{6}{z}}+\frac{\mathrm{7}{z}}{\mathrm{360}}−\frac{\mathrm{31}{z}^{\mathrm{3}} }{\mathrm{15120}}+… \\ $$
Commented by Olaf_Thorendsen last updated on 24/Jul/21
You are right mister. I forgot one term.
$$\mathrm{You}\:\mathrm{are}\:\mathrm{right}\:\mathrm{mister}.\:\mathrm{I}\:\mathrm{forgot}\:\mathrm{one}\:\mathrm{term}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *