Question Number 148445 by mathdanisur last updated on 28/Jul/21
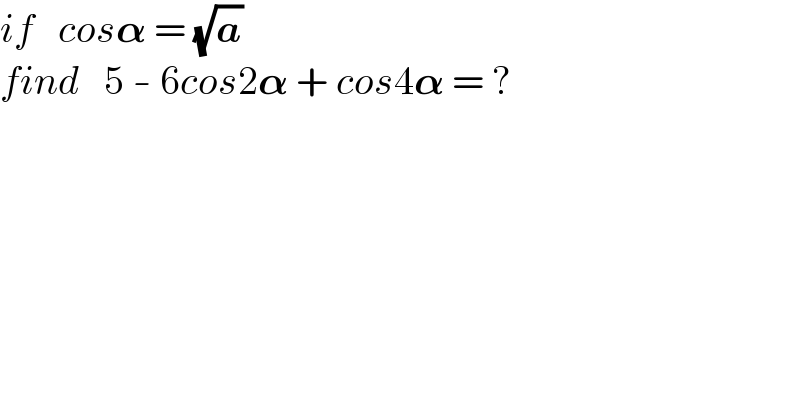
$${if}\:\:\:{cos}\boldsymbol{\alpha}\:=\:\sqrt{\boldsymbol{{a}}} \\ $$$${find}\:\:\:\mathrm{5}\:-\:\mathrm{6}{cos}\mathrm{2}\boldsymbol{\alpha}\:+\:{cos}\mathrm{4}\boldsymbol{\alpha}\:=\:? \\ $$
Commented by mathdanisur last updated on 28/Jul/21
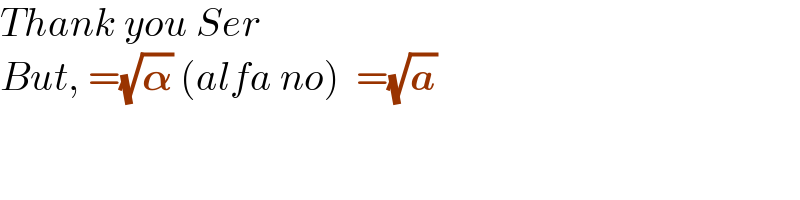
$${Thank}\:{you}\:{Ser} \\ $$$${But},\:=\sqrt{\boldsymbol{\alpha}}\:\left({alfa}\:{no}\right)\:\:=\sqrt{\boldsymbol{{a}}} \\ $$
Commented by mathdanisur last updated on 28/Jul/21
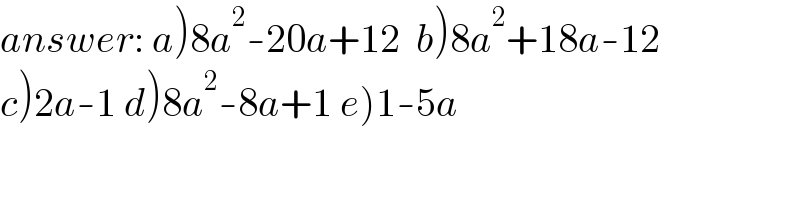
$$\left.{a}\left.{nswer}:\:{a}\right)\mathrm{8}{a}^{\mathrm{2}} -\mathrm{20}{a}+\mathrm{12}\:\:{b}\right)\mathrm{8}{a}^{\mathrm{2}} +\mathrm{18}{a}-\mathrm{12} \\ $$$$\left.{c}\left.\right)\left.\mathrm{2}{a}-\mathrm{1}\:{d}\right)\mathrm{8}{a}^{\mathrm{2}} -\mathrm{8}{a}+\mathrm{1}\:{e}\right)\mathrm{1}-\mathrm{5}{a} \\ $$
Commented by Olaf_Thorendsen last updated on 28/Jul/21
$$\mathrm{you}\:\mathrm{are}\:\mathrm{right}\:! \\ $$$$\mathrm{sorry}\:\mathrm{mister}. \\ $$$$\mathrm{my}\:\mathrm{eyes}\:\mathrm{are}\:\mathrm{very}\:\mathrm{old}. \\ $$
Answered by Olaf_Thorendsen last updated on 28/Jul/21
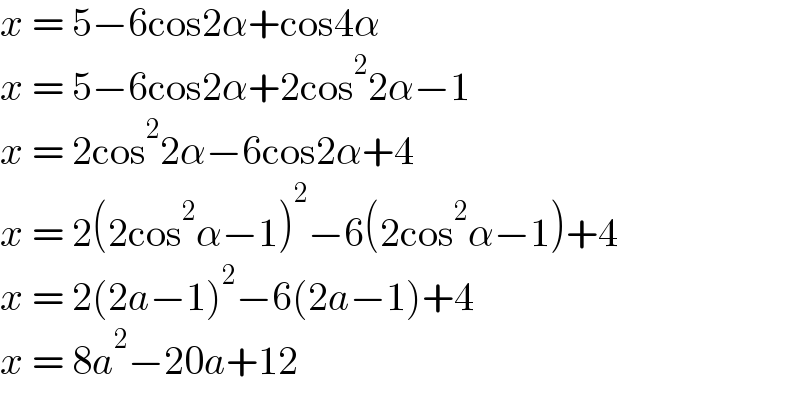
$${x}\:=\:\mathrm{5}−\mathrm{6cos2}\alpha+\mathrm{cos4}\alpha \\ $$$${x}\:=\:\mathrm{5}−\mathrm{6cos2}\alpha+\mathrm{2cos}^{\mathrm{2}} \mathrm{2}\alpha−\mathrm{1} \\ $$$${x}\:=\:\mathrm{2cos}^{\mathrm{2}} \mathrm{2}\alpha−\mathrm{6cos2}\alpha+\mathrm{4} \\ $$$${x}\:=\:\mathrm{2}\left(\mathrm{2cos}^{\mathrm{2}} \alpha−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{6}\left(\mathrm{2cos}^{\mathrm{2}} \alpha−\mathrm{1}\right)+\mathrm{4} \\ $$$${x}\:=\:\mathrm{2}\left(\mathrm{2}{a}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{6}\left(\mathrm{2}{a}−\mathrm{1}\right)+\mathrm{4} \\ $$$${x}\:=\:\mathrm{8}{a}^{\mathrm{2}} −\mathrm{20}{a}+\mathrm{12} \\ $$
Commented by mathdanisur last updated on 28/Jul/21
$${Thank}\:{you}\:{very}\:{much}\:{Sir} \\ $$
