Question Number 148534 by ajfour last updated on 28/Jul/21
Commented by ajfour last updated on 28/Jul/21
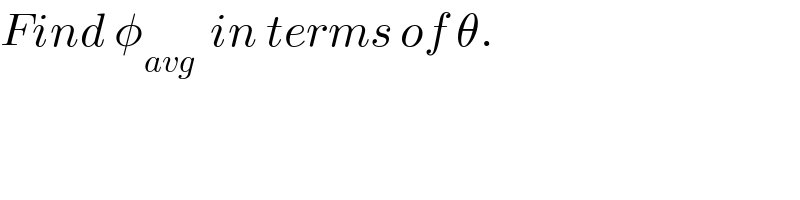
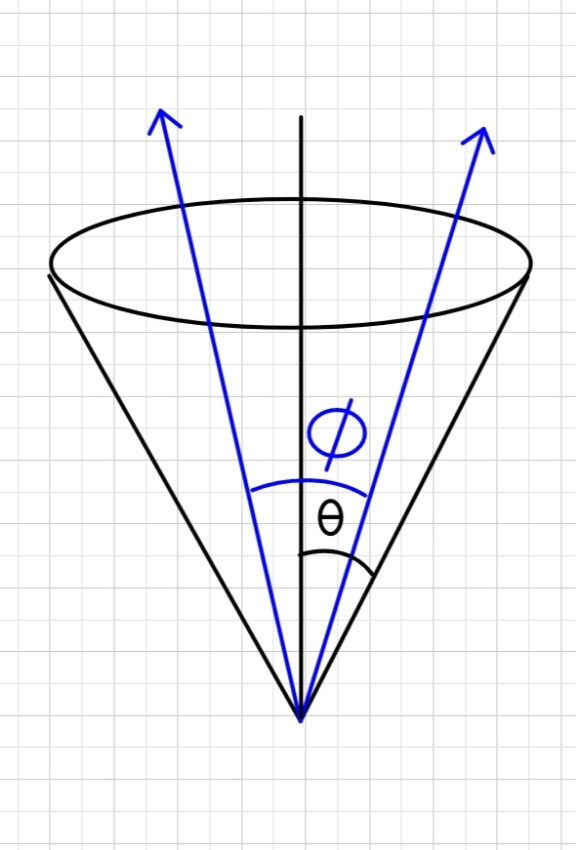
$${Find}\:\phi_{{avg}} \:\:{in}\:{terms}\:{of}\:\theta. \\ $$
Commented by MJS_new last updated on 29/Jul/21

$$\mathrm{I}\:\mathrm{think}\:\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{possible},\:\mathrm{because}\:\mathrm{it}'\mathrm{s}\:\mathrm{similar} \\ $$$$\mathrm{to}\:{Bertrand}'{s}\:{Paradox}\:\left(\mathrm{search}\:\mathrm{the}\:\mathrm{www}\right) \\ $$
Commented by ajfour last updated on 29/Jul/21
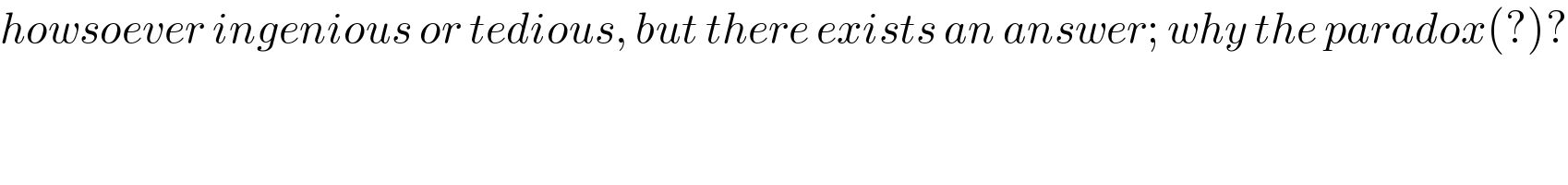
$${howsoever}\:{ingenious}\:{or}\:{tedious},\:{but}\:{there}\:{exists}\:{an}\:{answer};\:{why}\:{the}\:{paradox}\left(?\right)? \\ $$
Commented by MJS_new last updated on 29/Jul/21
https://en.m.wikipedia.org/wiki/Bertrand_paradox_(probability)
Commented by MJS_new last updated on 29/Jul/21

$$\mathrm{read}\:\mathrm{this} \\ $$
Commented by mr W last updated on 31/Jul/21

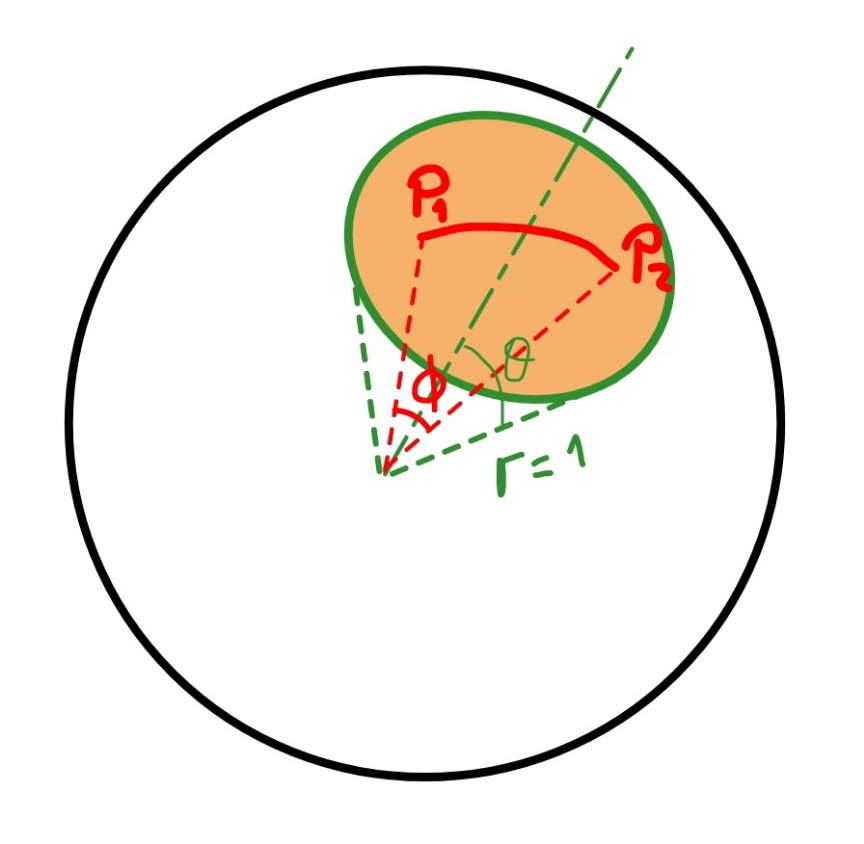
$${is}\:{it}\:{not}\:{the}\:{same}\:{as}\:{the}\:{question}\:{to} \\ $$$${find}\:{the}\:{average}\:{distance}\:{between} \\ $$$${two}\:{randomly}\:{selected}\:{points}\:{on}\:{a} \\ $$$${part}\:{of}\:{the}\:{surface}\:{of}\:{a}\:{sphere}\:{with} \\ $$$${unit}\:{radius}? \\ $$
Commented by mr W last updated on 31/Jul/21
Commented by ajfour last updated on 03/Aug/21
$${sir},\:{go}\:{ahead},\:{solve}\:{this},\:{i}\:{will} \\ $$$${try}\:{too}. \\ $$
Answered by ajfour last updated on 06/Aug/21
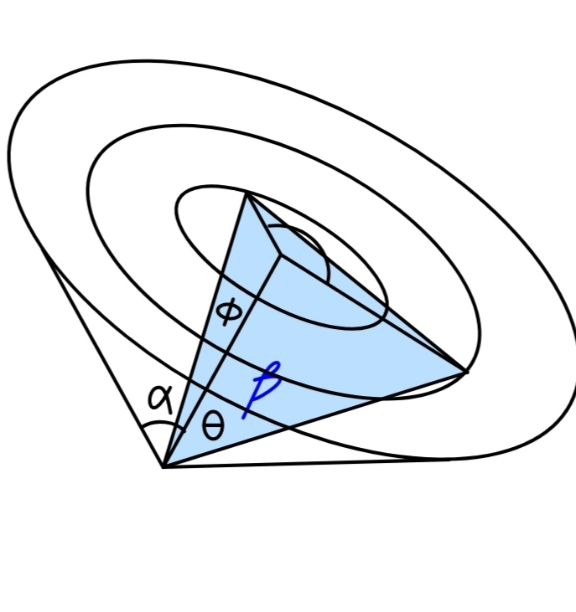
Commented by ajfour last updated on 06/Aug/21
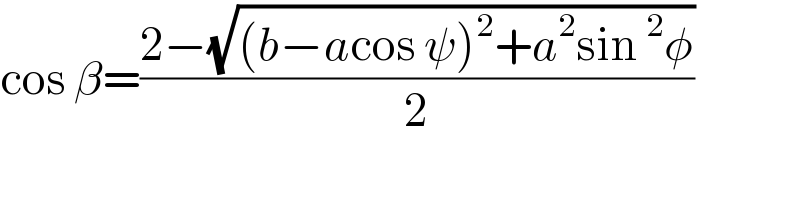
$$\mathrm{cos}\:\beta=\frac{\mathrm{2}−\sqrt{\left({b}−{a}\mathrm{cos}\:\psi\right)^{\mathrm{2}} +{a}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \phi}}{\mathrm{2}} \\ $$$$ \\ $$
