Question Number 148711 by Rankut last updated on 30/Jul/21

$${if}\:{x}+\frac{\mathrm{1}}{{x}}=\mathrm{4},\:{and}\:{x}−\frac{\mathrm{1}}{{x}}=\mathrm{3} \\ $$$${then}\:{prove}\:{that}\:\mathrm{4}=\mathrm{5} \\ $$
Answered by liberty last updated on 30/Jul/21

$$\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }+\mathrm{2}=\mathrm{16}\Rightarrow\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }=\mathrm{14} \\ $$$$\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }−\mathrm{2}=\mathrm{9}\Rightarrow\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }=\mathrm{11} \\ $$$$\mathrm{then}\:\mathrm{14}=\mathrm{11} \\ $$
Answered by liberty last updated on 30/Jul/21
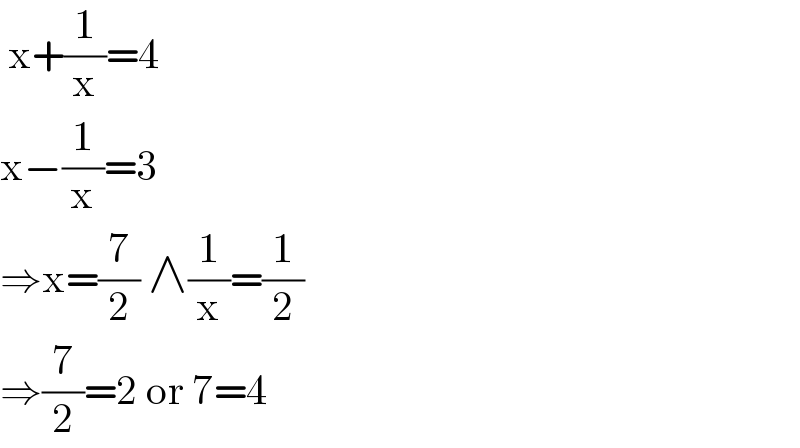
$$\:\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}=\mathrm{4} \\ $$$$\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}=\mathrm{3} \\ $$$$\Rightarrow\mathrm{x}=\frac{\mathrm{7}}{\mathrm{2}}\:\wedge\frac{\mathrm{1}}{\mathrm{x}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{7}}{\mathrm{2}}=\mathrm{2}\:\mathrm{or}\:\mathrm{7}=\mathrm{4}\: \\ $$
