Question Number 83188 by john santu last updated on 28/Feb/20
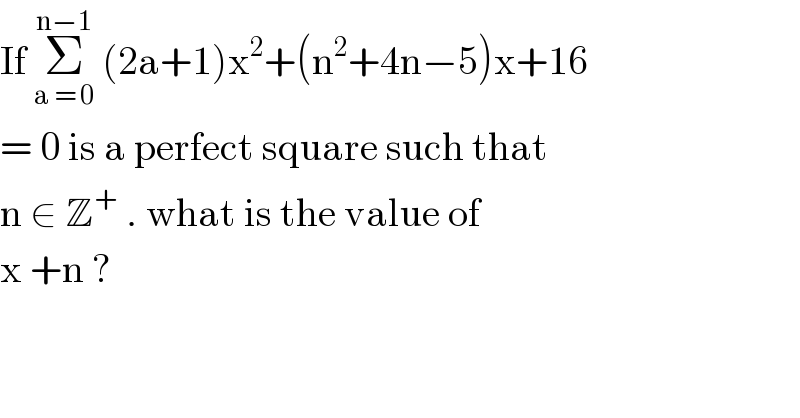
$$\mathrm{If}\:\underset{\mathrm{a}\:=\:\mathrm{0}} {\overset{\mathrm{n}−\mathrm{1}} {\sum}}\:\left(\mathrm{2a}+\mathrm{1}\right)\mathrm{x}^{\mathrm{2}} +\left(\mathrm{n}^{\mathrm{2}} +\mathrm{4n}−\mathrm{5}\right)\mathrm{x}+\mathrm{16} \\ $$$$=\:\mathrm{0}\:\mathrm{is}\:\mathrm{a}\:\mathrm{perfect}\:\mathrm{square}\:\mathrm{such}\:\mathrm{that}\: \\ $$$$\mathrm{n}\:\in\:\mathbb{Z}^{+} \:.\:\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\: \\ $$$$\mathrm{x}\:+\mathrm{n}\:?\: \\ $$
Answered by mind is power last updated on 01/Mar/20
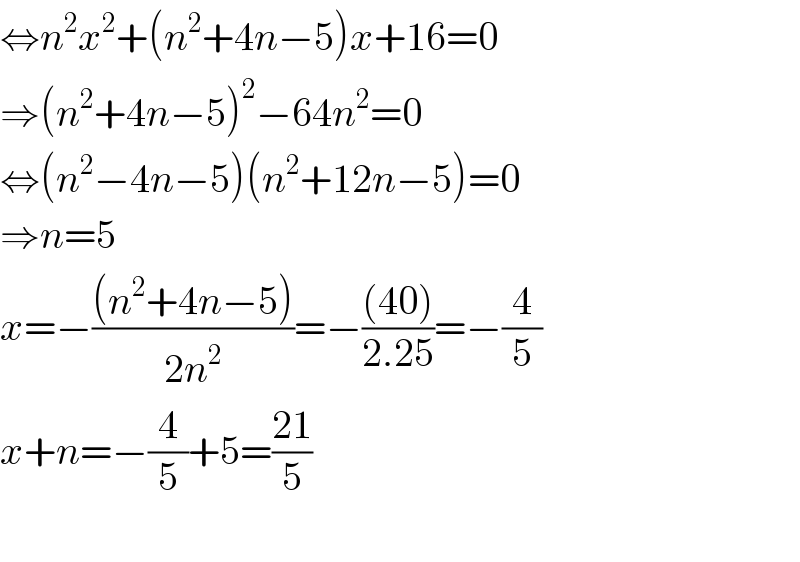
$$\Leftrightarrow{n}^{\mathrm{2}} {x}^{\mathrm{2}} +\left({n}^{\mathrm{2}} +\mathrm{4}{n}−\mathrm{5}\right){x}+\mathrm{16}=\mathrm{0} \\ $$$$\Rightarrow\left({n}^{\mathrm{2}} +\mathrm{4}{n}−\mathrm{5}\right)^{\mathrm{2}} −\mathrm{64}{n}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Leftrightarrow\left({n}^{\mathrm{2}} −\mathrm{4}{n}−\mathrm{5}\right)\left({n}^{\mathrm{2}} +\mathrm{12}{n}−\mathrm{5}\right)=\mathrm{0} \\ $$$$\Rightarrow{n}=\mathrm{5} \\ $$$${x}=−\frac{\left({n}^{\mathrm{2}} +\mathrm{4}{n}−\mathrm{5}\right)}{\mathrm{2}{n}^{\mathrm{2}} }=−\frac{\left(\mathrm{40}\right)}{\mathrm{2}.\mathrm{25}}=−\frac{\mathrm{4}}{\mathrm{5}} \\ $$$${x}+{n}=−\frac{\mathrm{4}}{\mathrm{5}}+\mathrm{5}=\frac{\mathrm{21}}{\mathrm{5}} \\ $$$$ \\ $$
