Question Number 67021 by mathmax by abdo last updated on 21/Aug/19
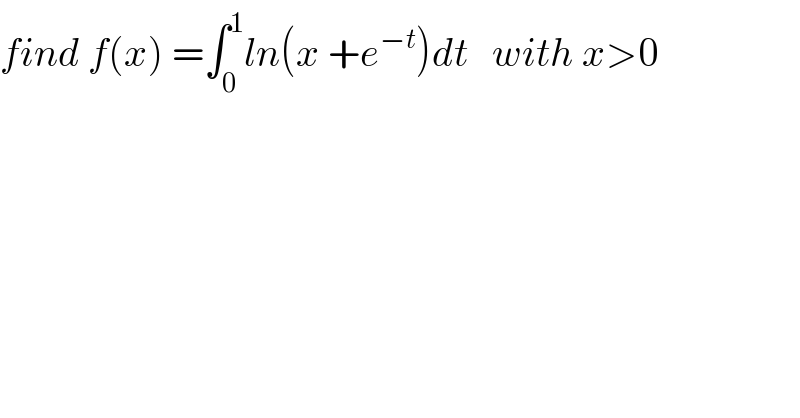
$${find}\:{f}\left({x}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left({x}\:+{e}^{−{t}} \right){dt}\:\:\:{with}\:{x}>\mathrm{0} \\ $$
Commented by mathmax by abdo last updated on 25/Aug/19
![we have f^′ (x) =∫_0 ^1 (dt/(x+e^(−t) ))dt =(1/x)∫_0 ^1 (dt/(1+(e^(−t) /x))) if x>1 we have f^′ (x) =(1/x)∫_0 ^1 Σ_(n=0) ^∞ (−1)^n ((e^(−t) /x))^n =Σ_(n=0) ^∞ (((−1)^n )/x^(n+1) ) ∫_0 ^1 e^(−nt) dt =(1/x)+Σ_(n=1) ^∞ (((−1)^n )/x^(n+1) )(−(1/n))[ e^(−nt) ]_0 ^1 =(1/x)−Σ_(n=1) ^∞ (((−1)^n )/(nx^(n+1) )){e^(−n) −1} =(1/x)−Σ_(n=1) ^∞ (((−e)^n )/(nx^(n+1) )) +Σ_(n=1) ^∞ (((−1)^n )/(nx^(n+1) )) ⇒ f(x) =ln(x)−Σ_(n=1) ^∞ (((−e)^n )/n) ∫_1 ^x (dt/t^(n+1) ) +Σ_(n=1) ^∞ (((−1)^n )/n)∫_1 ^x (dt/t^(n+1) ) +C ∫_1 ^x (dt/t^(n+1) ) =∫_1 ^x t^(−n−1) dt =[(1/(−n))t^(−n) ]_1 ^x =(1/n)(1−(1/x^n )) ⇒ f(x) =ln(x)−Σ_(n=1) ^∞ (((−e)^n )/n^2 )(1−(1/x^n ))+Σ_(n=1) ^∞ (((−1)^n )/n^2 )(1−(1/x^n ))+C C =f(1) =∫_0 ^1 ln(1+e^(−t) )dt ⇒ f(x)=ln(x)−Σ_(n=1) ^∞ (((−e)^n )/n^2 ) +Σ_(n=1) ^∞ (((−e)^n )/(n^2 x^n )) +Σ_(n=1) ^∞ (((−1)^n )/n^2 ) −Σ_(n=1) ^∞ (((−1)^n )/(n^2 x^n )) ....be continued....](https://www.tinkutara.com/question/Q67328.png)
$${we}\:{have}\:\:{f}^{'} \left({x}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dt}}{{x}+{e}^{−{t}} }{dt}\:=\frac{\mathrm{1}}{{x}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dt}}{\mathrm{1}+\frac{{e}^{−{t}} }{{x}}} \\ $$$${if}\:{x}>\mathrm{1}\:\:{we}\:{have}\:{f}^{'} \left({x}\right)\:=\frac{\mathrm{1}}{{x}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \left(\frac{{e}^{−{t}} }{{x}}\right)^{{n}} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{x}^{{n}+\mathrm{1}} }\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{−{nt}} {dt}\:=\frac{\mathrm{1}}{{x}}+\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{x}^{{n}+\mathrm{1}} }\left(−\frac{\mathrm{1}}{{n}}\right)\left[\:\:{e}^{−{nt}} \right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{{x}}−\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{nx}^{{n}+\mathrm{1}} }\left\{{e}^{−{n}} −\mathrm{1}\right\}\:=\frac{\mathrm{1}}{{x}}−\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−{e}\right)^{{n}} }{{nx}^{{n}+\mathrm{1}} }\:+\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{nx}^{{n}+\mathrm{1}} }\:\Rightarrow \\ $$$${f}\left({x}\right)\:={ln}\left({x}\right)−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−{e}\right)^{{n}} }{{n}}\:\int_{\mathrm{1}} ^{{x}} \:\frac{{dt}}{{t}^{{n}+\mathrm{1}} }\:+\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}\int_{\mathrm{1}} ^{{x}} \:\frac{{dt}}{{t}^{{n}+\mathrm{1}} }\:+{C} \\ $$$$\int_{\mathrm{1}} ^{{x}} \:\frac{{dt}}{{t}^{{n}+\mathrm{1}} }\:=\int_{\mathrm{1}} ^{{x}} \:{t}^{−{n}−\mathrm{1}} {dt}\:=\left[\frac{\mathrm{1}}{−{n}}{t}^{−{n}} \right]_{\mathrm{1}} ^{{x}} \:=\frac{\mathrm{1}}{{n}}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}^{{n}} }\right)\:\Rightarrow \\ $$$${f}\left({x}\right)\:={ln}\left({x}\right)−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−{e}\right)^{{n}} }{{n}^{\mathrm{2}} }\left(\mathrm{1}−\frac{\mathrm{1}}{{x}^{{n}} }\right)+\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{2}} }\left(\mathrm{1}−\frac{\mathrm{1}}{{x}^{{n}} }\right)+{C} \\ $$$${C}\:={f}\left(\mathrm{1}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{e}^{−{t}} \right){dt}\:\Rightarrow \\ $$$${f}\left({x}\right)={ln}\left({x}\right)−\sum_{{n}=\mathrm{1}} ^{\infty} \frac{\left(−{e}\right)^{{n}} }{{n}^{\mathrm{2}} }\:+\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−{e}\right)^{{n}} }{{n}^{\mathrm{2}} {x}^{{n}} }\:+\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{2}} } \\ $$$$−\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{2}} \:{x}^{{n}} }\:\:\:\:\:….{be}\:{continued}…. \\ $$$$ \\ $$
