Question Number 17704 by Tinkutara last updated on 09/Jul/17

$$\mathrm{A}\:\mathrm{monkey}\:\mathrm{climbs}\:\mathrm{up}\:\mathrm{a}\:\mathrm{slippery}\:\mathrm{pole}\:\mathrm{for} \\ $$$$\mathrm{3}\:\mathrm{seconds}\:\mathrm{and}\:\mathrm{subsequently}\:\mathrm{slips}\:\mathrm{for}\:\mathrm{3} \\ $$$$\mathrm{seconds}.\:\mathrm{Its}\:\mathrm{velocity}\:\mathrm{at}\:\mathrm{time}\:{t}\:\mathrm{is}\:\mathrm{given} \\ $$$$\mathrm{by}\:{v}\:\left({t}\right)\:=\:\mathrm{2}{t}\left(\mathrm{3}\:−\:{t}\right)\:;\:\mathrm{0}\:<\:{t}\:<\:\mathrm{3}\:\mathrm{and} \\ $$$${v}\:\left({t}\right)\:=\:−\:\left({t}\:−\:\mathrm{3}\right)\left(\mathrm{6}\:−\:{t}\right)\:\mathrm{for}\:\mathrm{3}\:<\:{t}\:<\:\mathrm{6}\:\mathrm{s} \\ $$$$\mathrm{in}\:\mathrm{m}/\mathrm{s}.\:\mathrm{It}\:\mathrm{repeats}\:\mathrm{this}\:\mathrm{cycle}\:\mathrm{till}\:\mathrm{it} \\ $$$$\mathrm{reaches}\:\mathrm{the}\:\mathrm{height}\:\mathrm{of}\:\mathrm{20}\:\mathrm{m}.\:\mathrm{At}\:\mathrm{what} \\ $$$$\mathrm{time}\:\mathrm{is}\:\mathrm{its}\:\mathrm{average}\:\mathrm{velocity}\:\mathrm{maximum}? \\ $$
Commented by ajfour last updated on 09/Jul/17

$$\mathrm{at}\:\boldsymbol{\mathrm{t}}=\frac{\mathrm{9}}{\mathrm{4}}\:\mathrm{s}\:. \\ $$
Answered by ajfour last updated on 09/Jul/17

Commented by ajfour last updated on 09/Jul/17
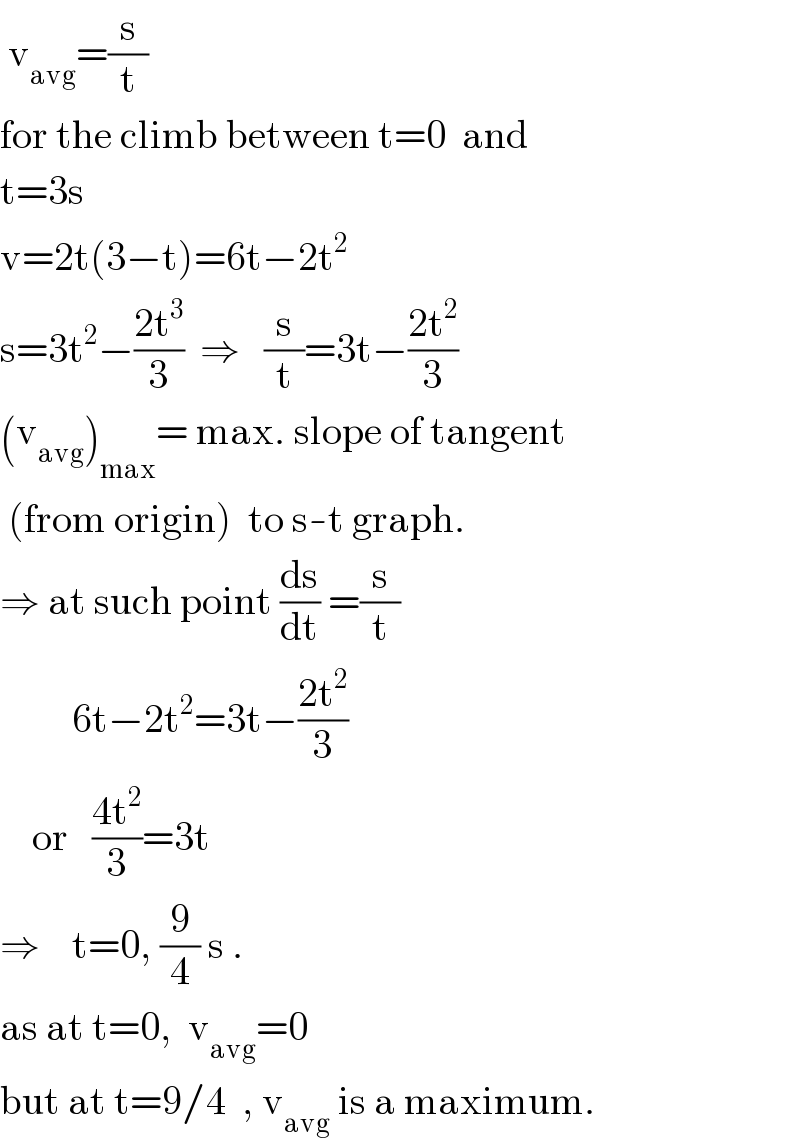
$$\:\mathrm{v}_{\mathrm{avg}} =\frac{\mathrm{s}}{\mathrm{t}} \\ $$$$\mathrm{for}\:\mathrm{the}\:\mathrm{climb}\:\mathrm{between}\:\mathrm{t}=\mathrm{0}\:\:\mathrm{and} \\ $$$$\mathrm{t}=\mathrm{3s} \\ $$$$\mathrm{v}=\mathrm{2t}\left(\mathrm{3}−\mathrm{t}\right)=\mathrm{6t}−\mathrm{2t}^{\mathrm{2}} \\ $$$$\mathrm{s}=\mathrm{3t}^{\mathrm{2}} −\frac{\mathrm{2t}^{\mathrm{3}} }{\mathrm{3}}\:\:\Rightarrow\:\:\:\frac{\mathrm{s}}{\mathrm{t}}=\mathrm{3t}−\frac{\mathrm{2t}^{\mathrm{2}} }{\mathrm{3}} \\ $$$$\left(\mathrm{v}_{\mathrm{avg}} \right)_{\mathrm{max}} =\:\mathrm{max}.\:\mathrm{slope}\:\mathrm{of}\:\mathrm{tangent}\: \\ $$$$\:\left(\mathrm{from}\:\mathrm{origin}\right)\:\:\mathrm{to}\:\mathrm{s}-\mathrm{t}\:\mathrm{graph}. \\ $$$$\Rightarrow\:\mathrm{at}\:\mathrm{such}\:\mathrm{point}\:\frac{\mathrm{ds}}{\mathrm{dt}}\:=\frac{\mathrm{s}}{\mathrm{t}} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{6t}−\mathrm{2t}^{\mathrm{2}} =\mathrm{3t}−\frac{\mathrm{2t}^{\mathrm{2}} }{\mathrm{3}} \\ $$$$\:\:\:\:\mathrm{or}\:\:\:\frac{\mathrm{4t}^{\mathrm{2}} }{\mathrm{3}}=\mathrm{3t}\:\: \\ $$$$\Rightarrow\:\:\:\:\mathrm{t}=\mathrm{0},\:\frac{\mathrm{9}}{\mathrm{4}}\:\mathrm{s}\:. \\ $$$$\mathrm{as}\:\mathrm{at}\:\mathrm{t}=\mathrm{0},\:\:\mathrm{v}_{\mathrm{avg}} =\mathrm{0} \\ $$$$\mathrm{but}\:\mathrm{at}\:\mathrm{t}=\mathrm{9}/\mathrm{4}\:\:,\:\mathrm{v}_{\mathrm{avg}} \:\mathrm{is}\:\mathrm{a}\:\mathrm{maximum}. \\ $$
Commented by Tinkutara last updated on 09/Jul/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
Answered by alex041103 last updated on 09/Jul/17
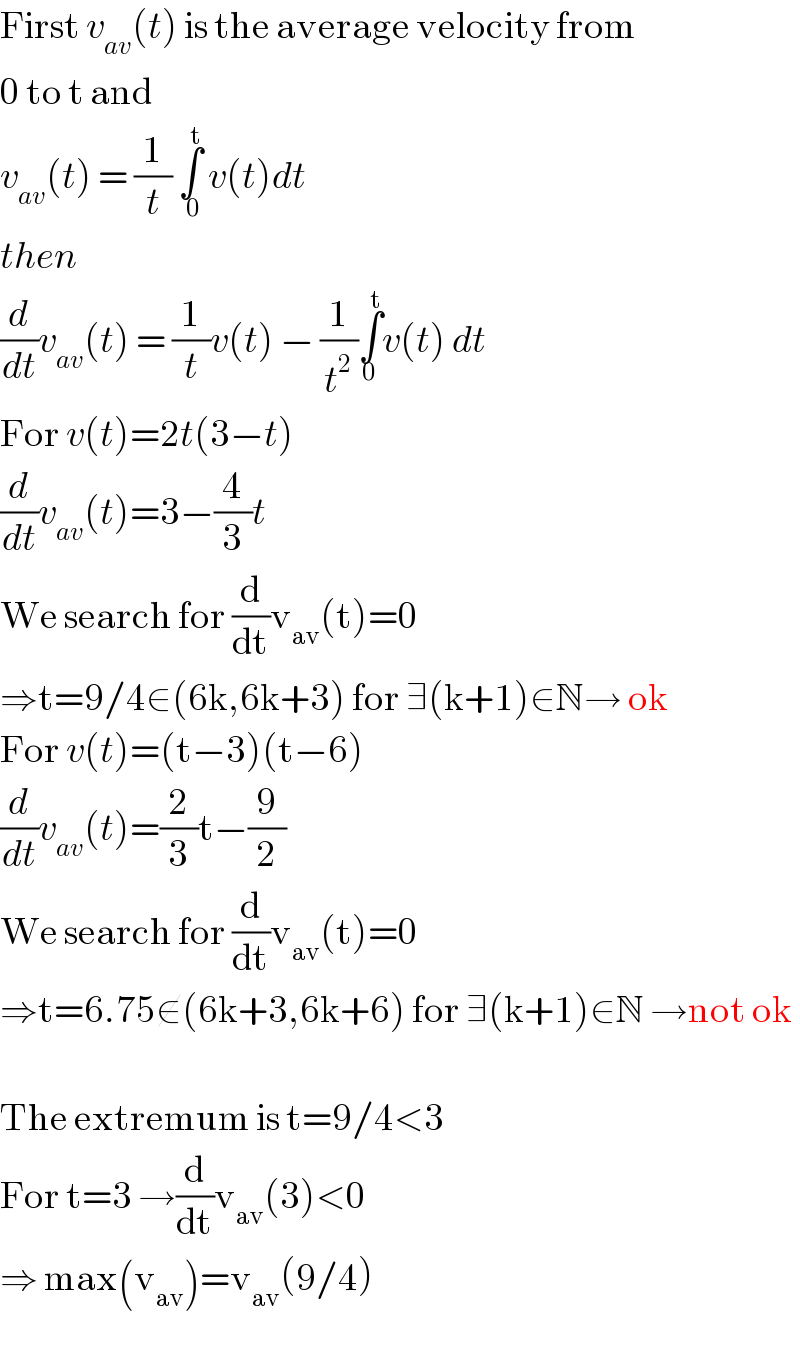
$$\mathrm{First}\:{v}_{{av}} \left({t}\right)\:\mathrm{is}\:\mathrm{the}\:\mathrm{average}\:\mathrm{velocity}\:\mathrm{from} \\ $$$$\mathrm{0}\:\mathrm{to}\:\mathrm{t}\:\mathrm{and} \\ $$$${v}_{{av}} \left({t}\right)\:=\:\frac{\mathrm{1}}{{t}}\:\underset{\:\:\mathrm{0}} {\overset{\mathrm{t}} {\int}}\:{v}\left({t}\right){dt} \\ $$$${then} \\ $$$$\frac{{d}}{{dt}}{v}_{{av}} \left({t}\right)\:=\:\frac{\mathrm{1}}{{t}}{v}\left({t}\right)\:−\:\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\underset{\mathrm{0}} {\overset{\mathrm{t}} {\int}}{v}\left({t}\right)\:{dt} \\ $$$$\mathrm{For}\:{v}\left({t}\right)=\mathrm{2}{t}\left(\mathrm{3}−{t}\right) \\ $$$$\frac{{d}}{{dt}}{v}_{{av}} \left({t}\right)=\mathrm{3}−\frac{\mathrm{4}}{\mathrm{3}}{t} \\ $$$$\mathrm{We}\:\mathrm{search}\:\mathrm{for}\:\frac{\mathrm{d}}{\mathrm{dt}}\mathrm{v}_{\mathrm{av}} \left(\mathrm{t}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{t}=\mathrm{9}/\mathrm{4}\in\left(\mathrm{6k},\mathrm{6k}+\mathrm{3}\right)\:\mathrm{for}\:\exists\left(\mathrm{k}+\mathrm{1}\right)\in\mathbb{N}\rightarrow\:\mathrm{ok} \\ $$$$\mathrm{For}\:{v}\left({t}\right)=\left(\mathrm{t}−\mathrm{3}\right)\left(\mathrm{t}−\mathrm{6}\right) \\ $$$$\frac{{d}}{{dt}}{v}_{{av}} \left({t}\right)=\frac{\mathrm{2}}{\mathrm{3}}\mathrm{t}−\frac{\mathrm{9}}{\mathrm{2}} \\ $$$$\mathrm{We}\:\mathrm{search}\:\mathrm{for}\:\frac{\mathrm{d}}{\mathrm{dt}}\mathrm{v}_{\mathrm{av}} \left(\mathrm{t}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{t}=\mathrm{6}.\mathrm{75}\notin\left(\mathrm{6k}+\mathrm{3},\mathrm{6k}+\mathrm{6}\right)\:\mathrm{for}\:\exists\left(\mathrm{k}+\mathrm{1}\right)\in\mathbb{N}\:\rightarrow\mathrm{not}\:\mathrm{ok} \\ $$$$ \\ $$$$\mathrm{The}\:\mathrm{extremum}\:\mathrm{is}\:\mathrm{t}=\mathrm{9}/\mathrm{4}<\mathrm{3} \\ $$$$\mathrm{For}\:\mathrm{t}=\mathrm{3}\:\rightarrow\frac{\mathrm{d}}{\mathrm{dt}}\mathrm{v}_{\mathrm{av}} \left(\mathrm{3}\right)<\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{max}\left(\mathrm{v}_{\mathrm{av}} \right)=\mathrm{v}_{\mathrm{av}} \left(\mathrm{9}/\mathrm{4}\right) \\ $$
Commented by Tinkutara last updated on 09/Jul/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
