Question Number 148819 by mathlove last updated on 31/Jul/21
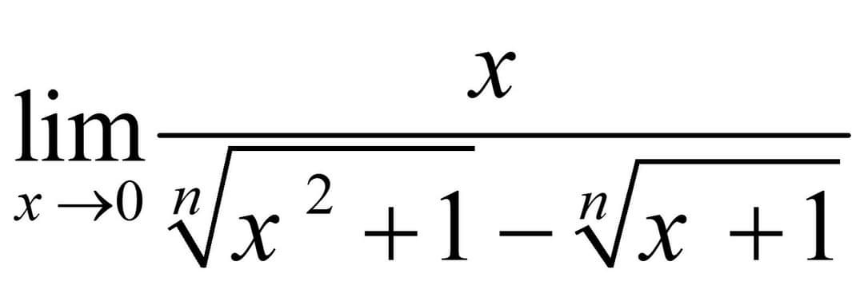
Answered by liberty last updated on 31/Jul/21
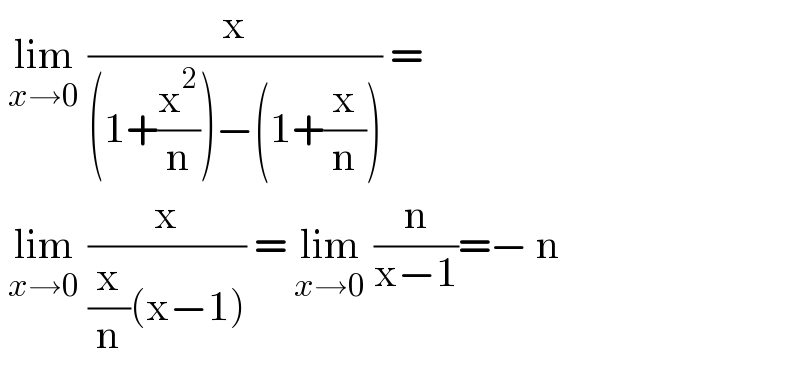
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{x}}{\left(\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{n}}\right)−\left(\mathrm{1}+\frac{\mathrm{x}}{\mathrm{n}}\right)}\:= \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{x}}{\frac{\mathrm{x}}{\mathrm{n}}\left(\mathrm{x}−\mathrm{1}\right)}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{n}}{\mathrm{x}−\mathrm{1}}=−\:\mathrm{n} \\ $$
Answered by Kamel last updated on 31/Jul/21
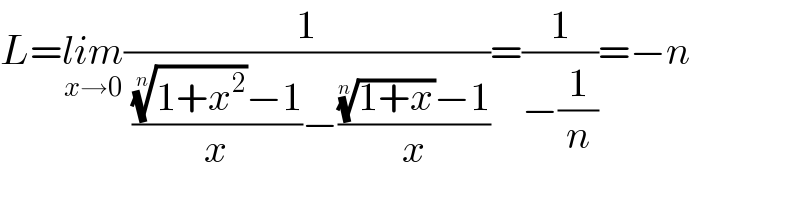
$${L}=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{\mathrm{1}}{\:\frac{\sqrt[{{n}}]{\mathrm{1}+{x}^{\mathrm{2}} }−\mathrm{1}}{{x}}−\frac{\sqrt[{{n}}]{\mathrm{1}+{x}}−\mathrm{1}}{{x}}}=\frac{\mathrm{1}}{−\frac{\mathrm{1}}{{n}}}=−{n} \\ $$
